（1）求高一年级、高二年级、高三年级分别抽取多少人？

（2）从13人中选出3人，求至少有1人认为个税起征点为4000元的概率；

（3）记从13人中选出3人中认为个税起征点为4000元的人数为，求的分布列与数学期望.

【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价（单位：元）和销售量（单位：万件）之间的一组数据，如下表所示：

（1）根据表中数据，建立关于的回归方程；

（2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在内，已知该产品的成本是元/件（其中），那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）

参考数据：，.

参考公式：，.

【题目】已知双曲线C： （a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， 点M与双曲线C的焦点不重合，点M关于F1 ， F2的对称点分别为A，B，线段MN的中点在双曲线的右支上，若|AN|﹣|BN|=12，则a=（ ）
A.3
B.4
C.5
D.6

【题目】将函数f（x）=2sin（ωx+ ）（ω＞0）的图象向右平移 个单位，得到函数y=g（x）的图象，若y=g（x）在[﹣ ， ]上为增函数，则ω的最大值为（ ）
A.3
B.2
C.
D.

【题目】某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用表示该学生选修的课程门数和没有选修的课程门数的乘积．

（1）记“函数为上的偶函数”为事件，求事件的概率；

（2）求的分布列和数学期望．

（1）求①②③④处分别对应的值；

（2）能有多大把握认为“高中生的性别与喜欢数学”有关？

附：

.

【题目】在△中，已知，直线经过点．

(Ⅰ)若直线:与线段交于点，且为△的外心，求△的外接圆的方程；

(Ⅱ)若直线方程为，且△的面积为，求点的坐标．

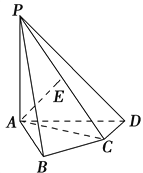
(1)证明：AE⊥平面PCD；

(2)求二面角A－PD－C的正弦值．

【题目】已知函数f（x）=|x﹣1|+|x﹣a|．
（1）若a=﹣1，解不等式f（x）≥3；
（2）如果x∈R，使得f（x）＜2成立，求实数a的取值范围．

【题目】在独立性检验中，统计量有三个临界值：2.706，3.841和6.635.当时，有90%的把握说明两个事件有关；当时，有95%的把握说明两个事件有关，当时，有99%的把握说明两个事件有关，当时，认为两个事件无关.在一项打鼾与心脏病的调查中，共调查了2000人，经计算.根据这一数据分析，认为打鼾与患心脏病之间（ ）

A. 有95%的把握认为两者有关 B. 约95%的打鼾者患心脏病

C. 有99%的把握认为两者有关 D. 约99%的打鼾者患心脏病