【题目】已知函数.

（1）当时，求该函数的定义域；

（2）当时，如果对任何都成立，求实数的取值范围；

（3）若，将函数的图像沿轴方向平移，得到一个偶函数的图像，设函数的最大值为，求的最小值.

【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比，比例系数为轮船的最大速度为15海里小时当船速为10海里小时，它的燃料费是每小时96元，其余航行运作费用（不论速度如何)总计是每小时150元假定运行过程中轮船以速度v匀速航行．

求k的值；

求该轮船航行100海里的总费用燃料费航行运作费用的最小值．

【题目】已知等差数列{an}满足：a1=2，且a1 ， a2 ， a5成等比数列．
（1）求数列{an}的通项公式；
（2）记Sn为数列{an}的前n项和，是否存在正整数n，使得Sn＞60n+800？若存在，求n的最小值；若不存在，说明理由．

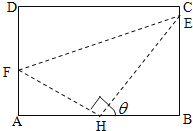
【题目】如图，某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道（，是直角顶点）来处理污水，管道越长，污水净化效果越好．设计要求管道的接口是的中点，分别落在线段上．已知米，米，记．

（1）试将污水净化管道的长度表示为的函数，并写出定义域；

（2）若，求此时管道的长度；

（3）当取何值时，污水净化效果最好？并求出此时管道的长度．

【题目】某次联欢会要安排个歌舞类节目、个小品类节目和个相声类节目的演出顺序，则同类节目不相邻的排法种数是（ ）

A. B. C. D.

【题目】对于定义域为的函数，如果同时满足以下三条：①对任意的，总有；②；③若，都有成立，则称函数为理想函数．

(1) 若函数为理想函数，求的值；

(2)判断函数是否为理想函数，并予以证明；

(3) 若函数为理想函数，假定，使得，且，求证：．

【题目】已知曲线C1的参数方程是(θ为参数)，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝－2cosθ.

(1)写出C1的极坐标方程和C2的直角坐标方程；

(2)已知点M1、M2的极坐标分别是(1，π)、(2，)，直线M1M2与曲线C2相交于P、Q两点，射线OP与曲线C1相交于点A，射线OQ与曲线C1相交于点B，求的值．

【题目】已知函数， ，在处的切线方程为.

（1）求， ；

（2）若，证明： .

【答案】（1）， ；（2）见解析

【解析】试题分析：（1）求出函数的导数，得到关于 的方程组，解出即可；

（2）由（1）可知， ，

由，可得，令， 利用导数研究其单调性可得

，

从而证明.

试题解析：（（1）由题意，所以，

又，所以，

若，则，与矛盾，故， .

（2）由（1）可知， ，

由，可得，

令，

，

令

当时， ， 单调递减，且；

当时， ， 单调递增；且，

所以在上当单调递减，在上单调递增，且，

故，

故.

【点睛】本题考查利用函数的切线求参数的方法，以及利用导数证明不等式的方法，解题时要认真审题，注意导数性质的合理运用.

【题型】解答题
【结束】
22

【题目】在平面直角坐标系中，曲线的参数方程为（， 为参数），以坐标原点为极点， 轴正半轴为极轴建立极坐标系，直线的极坐标方程为，若直线与曲线相切；

（1）求曲线的极坐标方程；

（2）在曲线上取两点， 与原点构成，且满足，求面积的最大值.

【题目】已知是定义在上的奇函数，且，若，时，有成立．

（1）判断在上的单调性，并证明；

（2）解不等式：；

（3）若对所有的恒成立，求实数的取值范围．

【题目】某实验室一天的温度（单位：℃）随时间t（单位：h）的变化近似满足函数关系：
f（t）=10﹣ ，t∈[0，24）
（1）求实验室这一天的最大温差；
（2）若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？