
科目: 来源: 题型:
【题目】厦门市从2003年起每年都举行国际马拉松比赛,每年马拉松比赛期间,都会吸引许多外地游客到厦门旅游,这将极大地推进厦门旅游业的发展,旅游部门将近六年马拉松比赛期间外地游客数量统计如下表:
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
比赛年份编号 |
|
|
|
|
|
|
外地游客人数 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;(精确到
的线性回归方程;(精确到![]() )
)
(2)若用对数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,且相关指数
,且相关指数![]() ,请用相关指数说明选择哪个模型更合适.(精确到
,请用相关指数说明选择哪个模型更合适.(精确到![]() )
)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
参考公式:回归方程![]() 中,
中, ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设实数c>0,整数p>1,n∈N* .
(1)证明:当x>﹣1且x≠0时,(1+x)p>1+px;
(2)数列{an}满足a1> ![]() ,an+1=
,an+1= ![]() an+
an+ ![]() an1﹣p . 证明:an>an+1>
an1﹣p . 证明:an>an+1> ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机调查![]() 名性别不同的大学生是否喜欢打羽毛球,得到如下
名性别不同的大学生是否喜欢打羽毛球,得到如下![]() 列联表:
列联表:
男 | 女 | 总计 | |
喜欢打羽毛球 |
|
|
|
不喜欢打羽毛球 |
|
|
|
总计 |
|
|
|
临界值表:
|
|
|
|
|
|
|
|
参考公式:![]() (其中
(其中![]() )
)
参照临界值表,下列结论正确的是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”
C. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
D. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q. 
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2 , l1与E1 , E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点. 
(1)证明:A1B1∥A2B2;
(2)过O作直线l(异于l1 , l2)与E1、E2分别交于C1、C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
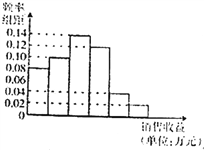
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益(单位:万元)绘制成如图所示的频率分布直方图.由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)该公司按照类似的研究方法,测得另外一些数据,并整理得到上表:
表中的数据显示![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若广告投入![]() 万元时,实际销售收益为
万元时,实际销售收益为![]() 万元,求残差
万元,求残差![]() .
.
附: ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() ;
;
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 上的距离的最小值的值.
上的距离的最小值的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=1+(1+a)x﹣x2﹣x3 , 其中a>0.
(1)讨论f(x)在其定义域上的单调性;
(2)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com