【题目】已知函数f（x）=|2x﹣a|+a．
（1）若不等式f（x）≤6的解集为{x|﹣2≤x≤3}，求实数a的值；
（2）在（1）的条件下，若存在实数n使f（n）≤m﹣f（﹣n）成立，求实数m的取值范围．

【题目】已知曲线C的极坐标方程为ρ=6sinθ，以极点O为原点，极轴为x轴的非负半轴建立直角坐标系，直线l的参数方程为 （t为参数）．
（1）求曲线C的直角坐标方程及直线l的普通方程；
（2）直线l与曲线C交于B，D两点，当|BD|取到最小值时，求a的值．

【题目】如图，在直三棱柱（侧棱垂直于底面）中，，，，.

（1）证明：平面；

（2）若是的中点，在线段上是否存在一点使平面？若存在，请确定点的位置；若不存在，也请说明理由.

【题目】已知函数
（1）当a=1时，求函数f（x）在x=e﹣1处的切线方程；
（2）当 时，讨论函数f（x）的单调性；
（3）若x＞0，求函数 的最大值．

【题目】已知椭圆C： （a＞b＞0）的两个焦点为F1 ， F2 ， 离心率为 ，点A，B在椭圆上，F1在线段AB上，且△ABF2的周长等于4 ．
（1）求椭圆C的标准方程；
（2）过圆O：x2+y2=4上任意一点P作椭圆C的两条切线PM和PN与圆O交于点M，N，求△PMN面积的最大值．

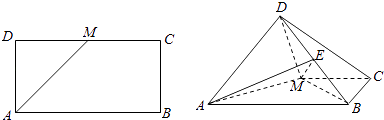
【题目】如图，已知长方形ABCD中，AB=2 ，AD= ，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM （Ⅰ）求证：AD⊥BM
（Ⅱ）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为 ．

【题目】在平面直角坐标系中，直线的参数方程为（为参数），，以原点为极点，轴正半轴为极轴建立极坐标系，圆极坐标方程为.

（1）若直线与圆相切，求的值；

（2）已知直线与圆交于，两点，记点、相应的参数分别为，，当时，求的长.

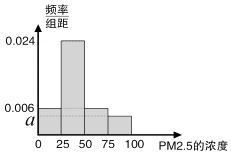
（1）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图． ①求图4中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列和数学期望．

【题目】已知函数，.

（1）问：能否为偶函数？请说明理由；

（2）总存在一个区间，当时，对任意的实数，方程无解，当时，存在实数，方程有解，求区间.

【题目】已知函数，.

（1）问：能否为偶函数？请说明理由；

（2）总存在一个区间，当时，对任意的实数，方程无解，当时，存在实数，方程有解，求区间.