【题目】在平面直角坐标系xOy中，曲线与x轴交于不同的两点A，B，曲线Γ与y轴交于点C．

（1）是否存在以AB为直径的圆过点C？若存在，求出该圆的方程;若不存在，请说明理由；

（2）求证:过A，B，C三点的圆过定点，并求出该定点的坐标．

【题目】如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4．设圆C的半径为1，圆心在l上．

（1）若圆心C也在直线y=x﹣1上，过点A作圆C的切线，求切线的方程；
（2）若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围．

【题目】如图，在三棱锥S﹣ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：

（1）平面EFG∥平面ABC；
（2）BC⊥SA．

【题目】已知 =（cosα，sinα）， =（cosβ，sinβ），0＜β＜α＜π．
（1）若| ﹣ |= ，求证： ⊥ ；
（2）设 =（0，1），若 + = ，求α，β的值．

【题目】在正项等比数列{an}中， ，a6+a7=3，则满足a1+a2+…+an＞a1a2…an的最大正整数n的值为 ．

【题目】已知函数（）在同一半周期内的图象过点， ， ，其中为坐标原点， 为函数图象的最高点， 为函数的图象与轴的正半轴的交点， 为等腰直角三角形.

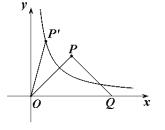
（1）求的值；

（2）将绕原点按逆时针方向旋转角，得到，若点恰好落在曲线（）上（如图所示），试判断点是否也落在曲线（）上，并说明理由.

【题目】甲、乙两人各射击一次，击中目标的概率分别是和.假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响.

（1）求甲射击4次，至少1次未击中目标的概率；

（2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率.

则成绩较为稳定（方差较小）的那位运动员成绩的方差为 ．

（1）通过画散点图，发现可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

（2）①建立月总成本y与月产量x之间的回归方程；

②通过建立的y关于x的回归方程，估计某月产量为1.98万件时，此时产品的总成本为多少万元？

（均精确到0.001）

附注：①参考数据：，

，

②参考公式：相关系数，

回归方程中斜率和截距的最小二乘估计公式分别为：．