
科目: 来源: 题型:
【题目】函数![]() 在
在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求函数的解析式.
(2)求函数的单调递增区间.
(3)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值);若不存在,请说明理由.
的范围(或值);若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个结论:
①从1,2,3,4,5中任取2个不同的数,事件![]() “取到的2个数之和为偶数”,事件
“取到的2个数之和为偶数”,事件![]() “取到的
“取到的
2个数均为偶数”,则![]() ;
;
②某班共有45名学生,其中30名男同学,15名女同学,老师随机抽查了5名同学的作业,用![]() 表示抽查到的女生的人数,则
表示抽查到的女生的人数,则![]() ;
;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④由直线![]() ,
,![]() ,曲线
,曲线![]() 及
及![]() 轴所围成的图形的面积是
轴所围成的图形的面积是![]() .
.
其中所有正确结论的序号为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,设底面ABCD是边长为1的正方形,PA⊥面ABCD. 
(1)求证:PC⊥BD;
(2)过BD且与直线PC垂直的平面与PC交于点E,当三棱锥E﹣BCD的体积最大时,求二面角E﹣BD﹣C的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望和方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: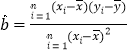 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
科目: 来源: 题型:
【题目】2017年10月9日,教育部考试中心下发了《关于![]() 年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了
年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中支持态度的为
人中支持态度的为![]() 人.
人.
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(1)完成![]() 列联表
列联表
(2)判断是否有![]() 的把握认为性别与支持有关?
的把握认为性别与支持有关?
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中, ![]() =λ
=λ ![]() (0<λ<1),cosC=
(0<λ<1),cosC= ![]() ,cos∠ADC=
,cos∠ADC= ![]() .
.
(1)若AC=5.BC=7,求AB的大小;
(2)若AC=7,BD=10,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com