【题目】已知函数f（x）= ．
（1）证明函数f（x）在（﹣1，+∞）上为单调递增函数；
（2）若x∈[0，2]，求函数f（x）的值域．

【题目】已知 ， 是非零不共线的向量，设 = + ，定义点集M={K| = }，当K1 ， K2∈M时，若对于任意的r≥2，不等式| |≤c| |恒成立，则实数c的最小值为 ．

【题目】若数列{an}中的项都满足a2n﹣1=a2n＜a2n+1（n∈N*），则称{an}为“阶梯数列”．
（1）设数列{bn}是“阶梯数列”，且b1=1，b2n+1=9b2n﹣1（n∈N*），求b2016；
（2）设数列{cn}是“阶梯数列”，其前n项和为Sn ， 求证：{Sn}中存在连续三项成等差数列，但不存在连续四项成等差数列；
（3）设数列{dn}是“阶梯数列”，且d1=1，d2n+1=d2n﹣1+2（n∈N*），记数列{ }的前n项和为Tn ， 问是否存在实数t，使得（t﹣Tn）（t+ ）＜0对任意的n∈N*恒成立？若存在，请求出实数t的取值范围；若不存在，请说明理由．

【题目】设函数f（x）=lnx﹣ax（a∈R）．
（1）若直线y=3x﹣1是函数f（x）图象的一条切线，求实数a的值；
（2）若函数f（x）在[1，e2]上的最大值为1﹣ae（e为自然对数的底数），求实数a的值；
（3）若关于x的方程ln（2x2﹣x﹣3t）+x2﹣x﹣t=ln（x﹣t）有且仅有唯一的实数根，求实数t的取值范围．

【题目】如图所示，有一块矩形空地ABCD，AB=2km，BC=4km，根据周边环境及地形实际，当地政府规划在该空地内建一个筝形商业区AEFG，筝形的顶点A，E，F，G为商业区的四个入口，其中入口F在边BC上（不包含顶点），入口E，G分别在边AB，AD上，且满足点A，F恰好关于直线EG对称，矩形内筝形外的区域均为绿化区．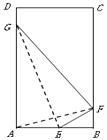

（1）请确定入口F的选址范围；
（2）设商业区的面积为S1 ， 绿化区的面积为S2 ， 商业区的环境舒适度指数为 ，则入口F如何选址可使得该商业区的环境舒适度指数最大？

【题目】如图，在四边形ABCD中，| |=4， =12，E为AC的中点．

（1）若cos∠ABC= ，求△ABC的面积S△ABC；
（2）若 =2 ，求 的值．

【题目】若函数在处取得极大值，则实数的取值范围是_____．

【题目】函数的零点个数为_____．

（1）求抛物线方程;

（2）直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.