
科目: 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。
(1)(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(2)(Ⅱ)求直线AF与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)(I)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可)
(2)(II)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
|
|
|
|
|
|
|
|
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立。根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一周期内的图像时,列表并填入的部分数据如下表:
在某一周期内的图像时,列表并填入的部分数据如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)请写出上表的![]() 及函数
及函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像上各点的横坐标缩小为原来的
个单位,再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的解析式及
的解析式及 的单调递增区间;
的单调递增区间;
(3)在(2)的条件下,若![]() 在
在![]() 上恰有奇数个零点,求实数
上恰有奇数个零点,求实数![]() 与零点个数
与零点个数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】
(2015·新课标Ⅱ)设函数f‘(x)是奇函数f(x)(x![]() R)的导函数,f(-1)=0,当x
R)的导函数,f(-1)=0,当x![]() 0时,xf'(x)-f(x)
0时,xf'(x)-f(x)![]() 0,则使得f(x)
0,则使得f(x)![]() 0成立的x的取值范围是()
0成立的x的取值范围是()
A.(-![]() ,-1)
,-1)![]() (0,1)
(0,1)
B.(-1,0)![]() (1,+
(1,+![]() )
)
C.(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
D.(0,1)![]() (1,+
(1,+![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
A.
B.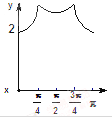
C.
D.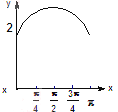
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则
设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则 ![]() +
+![]() >
>![]() +
+ ![]() ;(2)
;(2) ![]() +
+![]() >
> ![]() +
+ ![]() 是|a-b| < |c-d|的充要条件
是|a-b| < |c-d|的充要条件
(1)(I)若ab![]() cd,则
cd,则![]() +
+![]()
![]()
![]() +
+![]()
(2)(II)![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目: 来源: 题型:
【题目】如图O是等腰三角形ABC内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.
(1)(I)证明EF//BC
(2)(II)若AG等于圆O半径,且AE=MN=2![]() ,求四边形EBCF的面积
,求四边形EBCF的面积
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 已知f(x)=lnx+a(1-x),问:(1)讨论f(x) 的单调性;(2)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
已知f(x)=lnx+a(1-x),问:(1)讨论f(x) 的单调性;(2)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
(1)(I)讨论f(x) 的单调性;
(2)(II)当 f(x)有最大值,且最大值大于2a-2 时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com