
科目: 来源: 题型:
【题目】下列函数中,同时满足两个条件“①x∈R,f( ![]() +X)+f(
+X)+f( ![]() -X)=0;②当﹣
-X)=0;②当﹣ ![]() <x<
<x< ![]() 时,f′(x)>0”的一个函数是( )
时,f′(x)>0”的一个函数是( )
A.f(x)=sin(2x+ ![]() )
)
B.f(x)=cos(2x+ ![]() )
)
C.f(x)=sin(2x﹣ ![]() )
)
D.f(x)=cos(2x﹣ ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】以平面直角坐标系的原点为极点,以x轴的正半轴为极轴建立极坐标系.设曲线C的参数方程为 ![]() (α是参数),直线l的极坐标方程为ρcos(θ+
(α是参数),直线l的极坐标方程为ρcos(θ+ ![]() )=2
)=2 ![]() .
.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线l的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数发f(x)=(x+1)lnx﹣ax+2.
(1)当a=1时,求在x=1处的切线方程;
(2)若函数f(x)在定义域上具有单调性,求实数a的取值范围;
(3)求证: ![]() ,n∈N* .
,n∈N* .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C1: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,且过点
,且过点 ![]() ,直线l1:y=kx+m(m>0)与圆C2:(x﹣1)2+y2=1相切且与椭圆C1交于A,B两点. (Ⅰ)求椭圆C1的方程;
,直线l1:y=kx+m(m>0)与圆C2:(x﹣1)2+y2=1相切且与椭圆C1交于A,B两点. (Ⅰ)求椭圆C1的方程;
(Ⅱ)过原点O作l1的平行线l2交椭圆于C,D两点,设|AB|=λ|CD|,求λ的最小值.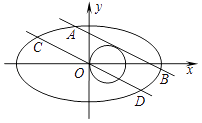
查看答案和解析>>
科目: 来源: 题型:
【题目】正三棱柱ABC﹣A1B1C1底边长为2,E,F分别为BB1 , AB的中点. (I)已知M为线段B1A1上的点,且B1A1=4B1M,求证:EM∥面A1FC;
(II)若二面角E﹣A1C﹣F所成角的余弦值为 ![]() ,求AA1的值.
,求AA1的值.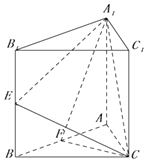
查看答案和解析>>
科目: 来源: 题型:
【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”? 参考公式: ![]() (n=a+b+c+d).
(n=a+b+c+d).
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 . (Ⅰ)若b+c=5,求b,c的值;
(Ⅱ)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,且满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 , 数列{ ![]() }的前n项和Tn , 若Tn<M对一切正整数n都成立,则M的最小值为 .
}的前n项和Tn , 若Tn<M对一切正整数n都成立,则M的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com