【题目】平面直角坐标系xOy中，过椭圆M： =1（a＞b＞0）焦点的直线x+y﹣2 =0交M于P，Q两点，G为PQ的中点，且OG的斜率为9．
（1）求M的方程；
（2）A、B是M的左、右顶点，C、D是M上的两点，若AC⊥BD，求四边形ABCD面积的最大值．

【题目】如图，四棱柱ABCD﹣A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，Q为BB1的中点，过A1 ， Q，D三点的平面记为α．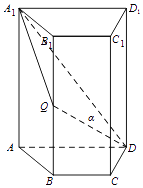
（1）证明：平面α与平面A1B1C1D1的交线平行于直线CD；
（2）若AA1=3，BC=CD= ，∠BCD=120°，求平面α与底面ABCD所成二面角的大小．

（1）已知甲、乙两人分别选择了产品A和产品B进行投资，如果一年后他们中至少有一人获利的概率大于 ，求p的取值范围；
（2）丙要将家中闲置的10万元钱进行投资，以一年后投资收益的期望值为决策依据，在产品A和产品B之中选其一，应选用哪个？

【题目】已知△ABC的内角A，B，C所对的边分别为a，b，c，且A=2C．
（1）若△ABC为锐角三角形，求 的取值范围；
（2）若b=1，c=3，求△ABC的面积．

【题目】已知命题p：函数f（x）= 是奇函数，命题q：函数g（x）=x3﹣x2在区间（0，+∞）上单调递增．则下列命题中为真命题的是（ ）
A.p∨q
B.p∧q
C.￢p∧q
D.￢p∨q

【题目】某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（ ）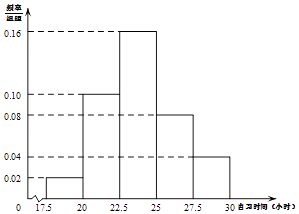
A.26.25
B.26.5
C.26.75
D.27

【题目】已知曲线C1的参数方程为 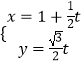（为参数）．在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线C2： ． （Ⅰ）求曲线C1的普通方程和C2的直角坐标方程；
（Ⅱ）若C1与C2相交于A、B两点，设点F（1，0），求 的值．

【题目】已知函数f（x）=（x﹣1）lnx﹣（x﹣a）2（a∈R）． （Ⅰ）若f（x）在（0，+∞）上单调递减，求a的取值范围；
（Ⅱ）若f（x）有两个极值点x1 ， x2 ， 求证：x1+x2＞ ．

【题目】已知 ()是偶函数，当时， ．

(1) 求的解析式；

(2) 若不等式在时都成立，求m的取值范围．