【题目】已知椭圆 抛物线 焦点均在 轴上， 的中心和 顶点均为原点 ，从每条曲线上各取两个点，将其坐标记录于表中，则 的左焦点到 的准线之间的距离为（ ）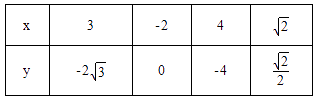

A.
B.
C.1
D.2

【题目】已知等比数列 前 项和为 ，则下列一定成立的是（ ）
A.若 ，则 ；
B.若 ，则 ；
C.若 ，则 ；
D.若 ，则 ．

【题目】“抛物线 的准线方程为 ”是“抛物线 的焦点与双曲线 的焦点重合”的（ ）
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

【题目】已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．
（1）求证：2a+b=2；
（2）若a+2b≥tab恒成立，求实数t的最大值．

【题目】在平面直角坐标系xOy中，直线l的参数方程为 （t为参数，0≤α＜π），以坐标原点O为极点，x轴的正半轴为极轴，并取相同的长度单位，建立极坐标系．曲线C1：p=1．
（1）若直线l与曲线C1相交于点A，B，点M（1，1），证明：|MA||MB|为定值；
（2）将曲线C1上的任意点（x，y）作伸缩变换 后，得到曲线C2上的点（x'，y'），求曲线C2的内接矩形ABCD周长的最大值．

【题目】已知f（x）=ln（ax+b）+x2（a≠0）．
（1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=x，求a，b的值；
（2）若f（x）≤x2+x恒成立，求ab的最大值．

【题目】已知过抛物线E：x2=2py（p＞0）焦点F且倾斜角的60°直线l与抛物线E交于点M，N，△OMN的面积为4．
（1）求抛物线E的方程；
（2）设P是直线y=﹣2上的一个动点，过P作抛物线E的切线，切点分别为A、B，直线AB与直线OP、y轴的交点分别为Q、R，点C、D是以R为圆心、RQ为半径的圆上任意两点，求∠CPD最大时点P的坐标．

【题目】如图所示，四面体ABCD中，已知平面BCD⊥平面ABC，BD⊥DC，BC=6，AB=4 ，∠ABC=30°．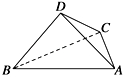
（1）求证：AC⊥BD；
（2）若二面角B﹣AC﹣D为45°，求直线AB与平面ACD所成的角的正弦值．

【题目】当今信息时代，众多中小学生也配上了手机．某机构为研究经常使用手机是否对学习成绩有影响，在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩，用茎叶图表示如图：
（1）根据茎叶图中的数据完成下面的2×2列联表，并判断是否有95%的把握认为经常使用手机对学习成绩有影响？

（2）从50人中，选取一名很少使用手机的同学（记为甲）和一名经常使用手机的同学（记为乙）解一道函数题，甲、乙独立解决此题的概率分别为P1 ， P2 ， P2=0.4，若P1﹣P2≥0.3，则此二人适合为学习上互帮互助的“对子”，记X为两人中解决此题的人数，若E（X）=1.12，问两人是否适合结为“对子”？ 参考公式及数据： ，其中n=a+b+c+d

【题目】已知△ABC的内角A，B，C的对边分别为a，b，c，且ctanC= （acosB+bcosA）．
（1）求角C；
（2）若c=2 ，求△ABC面积的最大值．