
科目: 来源: 题型:
【题目】在△ABC所在的平面内,点P0、P满足 ![]() =
= ![]()
![]() ,
, ![]() ,且对于任意实数λ,恒有
,且对于任意实数λ,恒有 ![]()
![]() ,则( )
,则( )
A.∠ABC=90°
B.∠BAC=90°
C.AC=BC
D.AB=AC
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若 ![]() ,其中m,n∈R.则m+n的取值范围是( )
,其中m,n∈R.则m+n的取值范围是( )
A.(0,1)
B.(﹣1,0)
C.(1,+∞)
D.(﹣∞,﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学在上学路上要经过A、B、C三个带有红绿灯的路口.已知他在A、B、C三个路口遇到红灯的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥A﹣BOC中,OA,OB,OC两两垂直,点D,E分别为棱BC,AC的中点,F在棱AO上,且满足OF= ![]() ,已知OA=OC=4,OB=2.
,已知OA=OC=4,OB=2.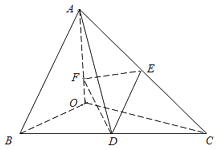
(1)求异面直线AD与OC所成角的余弦值;
(2)求二面角C﹣EF﹣D的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a>0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
(t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(ax﹣1)ex(a≠0,e是自然对数的底数).
(1)若函数f(x)在区间[1,2]上是单调减函数,求实数a的取值范围;
(2)求函数f(x)的极值;
(3)设函数f(x)图象上任意一点处的切线为l,求l在x轴上的截距的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足Sn=2an﹣1,n∈N*.数列{bn}满足nbn+1﹣(n+1)bn=n(n+1),n∈N*,且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an ![]() ,数列{cn}的前n项和为Tn , 对任意的n∈N*,都有Tn<nSn﹣a,求实数a的取值范围;
,数列{cn}的前n项和为Tn , 对任意的n∈N*,都有Tn<nSn﹣a,求实数a的取值范围;
(3)是否存在正整数m,n使b1 , am , bn(n>1)成等差数列,若存在,求出所有满足条件的m,n,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左顶点为A(﹣2,0),离心率为
=1(a>b>0)的左顶点为A(﹣2,0),离心率为 ![]() ,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.
,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.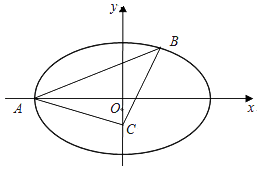
(1)求椭圆E的标准方程;
(2)若△ABC是以点C为直角顶点的等腰直角三角形,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且 ![]() ,设∠BOC=θ.
,设∠BOC=θ.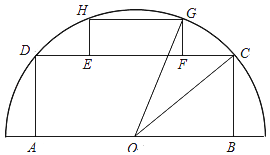
(1)记游泳池及其附属设施的占地面积为f(θ),求f(θ)的表达式;
(2)怎样设计才能符合园林局的要求?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA=SC,AB⊥AC,D为BC的中点,E为AC上一点,且DE∥平面SAB.求证: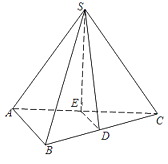
(1)直线AB∥平面SDE;
(2)平面ABC⊥平面SDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com