
科目: 来源: 题型:
【题目】已知坐标平面上动点 ![]() 与两个定点
与两个定点 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求点 ![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为 ![]() ,过点
,过点 ![]() 的直线
的直线 ![]() 被
被 ![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来郑州空气污染较为严重,现随机抽取一年(365天)内100天的空气中 ![]() 指数的监测数据,统计结果如下:
指数的监测数据,统计结果如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失为 ![]() (单位:元),
(单位:元), ![]() 指数为
指数为 ![]() .当
.当 ![]() 在区间
在区间 ![]() 内时对企业没有造成经济损失;当
内时对企业没有造成经济损失;当 ![]() 在区间
在区间 ![]() 内时对企业造成经济损失成直线模型(当
内时对企业造成经济损失成直线模型(当 ![]() 指数为150时造成的经济损失为500元,当
指数为150时造成的经济损失为500元,当 ![]() 指数为200 时,造成的经济损失为700元);当
指数为200 时,造成的经济损失为700元);当 ![]() 指数大于300时造成的经济损失为2000元.
指数大于300时造成的经济损失为2000元.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
(1)试写出 ![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失 ![]() 大于500元且不超过900元的概率;
大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面列联表,并判断是否有 ![]() 的把握认为郑州市本年度空气重度污染与供暖有关?
的把握认为郑州市本年度空气重度污染与供暖有关?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面梯形
中,底面梯形 ![]() ,
, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等边三角形,已知
是等边三角形,已知 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上任意一点,
上任意一点, ![]() ,且
,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)试确定 ![]() 的值,使三棱锥
的值,使三棱锥 ![]() 体积为三棱锥
体积为三棱锥 ![]() 体积的3倍.
体积的3倍.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图直三棱柱 ![]() 中,
中, ![]() 为边长为2的等边三角形,
为边长为2的等边三角形, ![]() ,点
,点 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 分别是边
分别是边 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的中点,动点
的中点,动点 ![]() 在四边形
在四边形 ![]() 内部运动,并且始终有
内部运动,并且始终有 ![]() 平面
平面 ![]() ,则动点
,则动点 ![]() 的轨迹长度为( )
的轨迹长度为( )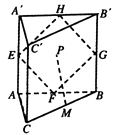
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们可以用随机模拟的方法估计 ![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数 ![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生 ![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为 ![]() ,则由此可估计
,则由此可估计 ![]() 的近似值为( )
的近似值为( )
A.3.119
B.3.124
C.3.132
D.3.151
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=a·2x+b·3x , 其中常数a,b满足ab≠0.
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t , 使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x);
(2)若不等式 ![]() -m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图象过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com