
科目: 来源: 题型:
【题目】若函数![]() 在
在![]() 上存在唯一的
上存在唯一的![]() 满足
满足![]() , 那么称函数
, 那么称函数![]() 是
是![]() 上的“单值函数”.已知函数
上的“单值函数”.已知函数![]() 是
是![]() 上的“单值函数”,当实数
上的“单值函数”,当实数![]() 取最小值时,函数
取最小值时,函数![]() 在
在![]() 上恰好有两点零点,则实数
上恰好有两点零点,则实数![]() 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示:
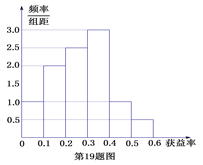
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在![]() 元的基础上每增加
元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下![]() 组
组![]() 与
与![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量![]() (万份)与
(万份)与![]() (元)的回归方程为
(元)的回归方程为![]() ;
;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: 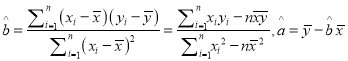
查看答案和解析>>
科目: 来源: 题型:
【题目】已知下列命题:
①命题“![]() ,
, ![]() ”的否定是:“
”的否定是:“![]() ,
, ![]() ”;
”;
②若样本数据![]() 的平均值和方差分别为
的平均值和方差分别为![]() 和
和![]() 则数据
则数据![]() 的平均值和标准差分别为
的平均值和标准差分别为![]() ,
, ![]() ;
;
③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件;
④在![]() 列联表中,若比值
列联表中,若比值![]() 与
与![]() 相差越大,则两个分类变量有关系的可能性就越大.
相差越大,则两个分类变量有关系的可能性就越大.
⑤已知![]() 为两个平面,且
为两个平面,且![]() ,
, ![]() 为直线.则命题:“若
为直线.则命题:“若![]() ,则
,则![]() ”的逆命题和否命题均为假命题.
”的逆命题和否命题均为假命题.
⑥设定点![]() 、
、![]() ,动点
,动点![]() 满足条件
满足条件![]() 为正常数),则
为正常数),则![]() 的轨迹是椭圆.其中真命题的个数为( )
的轨迹是椭圆.其中真命题的个数为( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
【答案】(I)证明见解析;(II)![]() ;(III)2018.
;(III)2018.
【解析】试题分析:
(1)左右两侧做差,结合代数式的性质可证得![]() ,即对
,即对![]() ,恒有:
,恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,给定特殊值,令
,给定特殊值,令![]() ,从而可得:
,从而可得:![]() ,则
,则![]() ,
,![]() ,从而有
,从而有![]() 恒成立,据此可知
恒成立,据此可知![]() ,则
,则![]() .
.
(3)结合(1)(2)的结论整理计算可得:![]() ,据此分组求和有:
,据此分组求和有:![]() .
.
试题解析:
(1)![]() (仅当
(仅当![]() 时,取“=”)
时,取“=”)
所以恒有:![]() 成立;
成立;
(2)由已知条件可设![]() ,则
,则![]() 中,令
中,令![]() ,
,
从而可得:![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因为![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,不合题意舍去,
,不合题意舍去,
当![]() 时,即
时,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(3)![]() ,
,
所以![]() ,
,
即![]() .
.
【题型】解答题
【结束】
22
【题目】已知函数![]() 为定义在
为定义在![]() 上的奇函数.
上的奇函数.
(1)求函数![]() 的值域;
的值域;
(2)当![]() 时,不等式
时,不等式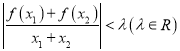 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车的推广给消费者带来全新消费体验,迅速赢得广大消费者的青睐,然而,同时也暴露出管理、停放、服务等方面的问题,为了了解公众对共享单车的态度(提倡或不提倡),某调查小组随机地对不同年龄段50人进行调查,将调查情况整理如下表:

并且,年龄在![]() 和
和![]() 的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
(Ⅰ)求年龄在![]() 中被抽到的2人都持“提倡”态度的概率;
中被抽到的2人都持“提倡”态度的概率;
(Ⅱ)求年龄在![]() 中被抽到的2人至少1人持“提倡”态度的概率.
中被抽到的2人至少1人持“提倡”态度的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com