
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
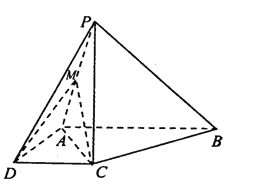
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目: 来源: 题型:
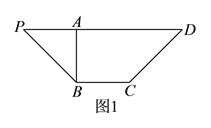
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
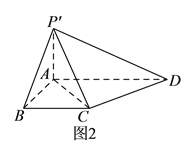
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值![]() 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来许多地市空气污染较为严重,现随机抽取某市一年(365天)内100天的![]() 空气质量指数(
空气质量指数(![]() )的监测数据,统计结果如表:
)的监测数据,统计结果如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 4 | 13 | 18 | 30 | 20 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时,对企业没有造成经济损失;当
内时,对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时,对企业造成的经济损失与
内时,对企业造成的经济损失与![]() 成直线模型(当
成直线模型(当![]() 指数为150时,造成的经济损失为1100元,当
指数为150时,造成的经济损失为1100元,当![]() 指数为200时,造成的经济损失为1400元);当
指数为200时,造成的经济损失为1400元);当![]() 指数大于300时,造成的经济损失为2000元.
指数大于300时,造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取1天,该天经济损失![]() 大于1100且不超过1700元的概率;
大于1100且不超过1700元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,这30天中有8天为严重污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该市本年度空气严重污染与供暖有关?
的把握认为该市本年度空气严重污染与供暖有关?
非严重污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位:千克)全部介于![]() 至
至![]() 之间,将数据分成以下
之间,将数据分成以下![]() 组,第一组
组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组,第五组
,第四组,第五组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第![]() 、
、![]() 、
、![]() 组中随机抽取
组中随机抽取![]() 名学生做初检.
名学生做初检.
(Ⅰ)求每组抽取的学生人数.
(Ⅱ)若从![]() 名学生中再次随机抽取
名学生中再次随机抽取![]() 名学生进行复检,求这
名学生进行复检,求这![]() 名学生不在同一组的概率.
名学生不在同一组的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.

(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P B1C1F的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD, ![]() ,M为PC的中点,N点在AB上且
,M为PC的中点,N点在AB上且![]() .
.
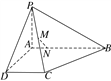
(1)证明:MN∥平面PAD;
(2)求直线MN与平面PCB所成的角.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图与侧视图是腰长为6的等腰直角三角形,俯视图是正方形.
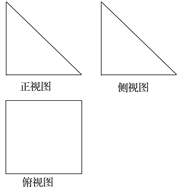
(1)请画出该几何体的直观图,并求出它的体积;
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼?试证明你的结论;
(3)在(2)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)设![]() ,点
,点![]() 是函数
是函数![]() 与
与![]() 的一个交点,且函数
的一个交点,且函数![]() 与
与![]() 在点
在点![]() 处的切线互相垂直,求证:存在唯一的
处的切线互相垂直,求证:存在唯一的![]() 满足题意,且
满足题意,且![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com