
科目: 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 的角平分线所在的直线
的角平分线所在的直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() 为椭圆
为椭圆![]() 上的一点,当
上的一点,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
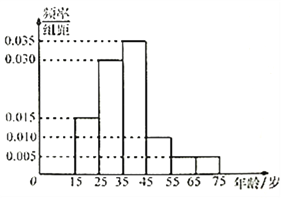
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式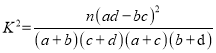 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为非零常数.
为非零常数.
(1)若![]() ,
, ![]() ,求证:
,求证: ![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公差不等于零的等差数列.
是公差不等于零的等差数列.
①求实数![]() ,
, ![]() 的值;
的值;
②数列![]() 的前
的前![]() 项和
项和![]() 构成数列
构成数列![]() ,从
,从![]() 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为![]() 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已经函数![]() 的定义域为
的定义域为![]() ,设
,设![]()
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数
上为单调函数
(2)求证![]()
(3)若不等式![]() (为
(为![]() 正整数)对任意正实数
正整数)对任意正实数![]() 恒成立,求
恒成立,求![]() 的最大值.(解答过程可参考使用以下数据
的最大值.(解答过程可参考使用以下数据![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】给定椭圆![]() ,称圆
,称圆![]() 为椭圆
为椭圆![]() 的“伴随圆”.已知点
的“伴随圆”.已知点![]() 是椭圆
是椭圆![]() 上的点
上的点
(1)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长:
所截得的弦长:
(2)![]() 是椭圆
是椭圆![]() 上的两点,设
上的两点,设![]() 是直线
是直线![]() 的斜率,且满足
的斜率,且满足![]() ,试问:直线
,试问:直线![]() 是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】我校为丰富师生课余活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的
(平方米)的![]() 矩形健身场地,如图,点
矩形健身场地,如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() ,
, ![]() 米,
米, ![]() 米,
米, ![]() .设矩形
.设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正常数)
为正常数)
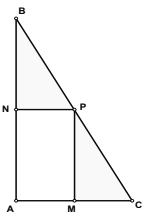
(1)试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ;
;
(3)如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价)
最低(不要求求出最低造价)
查看答案和解析>>
科目: 来源: 题型:
【题目】金砖国家领导人第九次会晤于2017年9月3日至5日在中国福建厦门市举行,为了在金砖峰会期间为来到厦门的外国嘉宾提供服务,培训部对两千余名志愿者进行了集中培训,为了检验培训效果,现培训部从两千余名志愿者中随机抽取100名,按年龄(单位:岁)分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
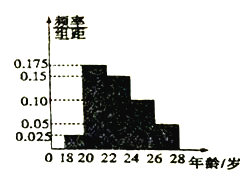
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者前去机场参加接待外宾礼仪测试,则应从第3,4,5组中各抽取多少名志愿者?
(2)在(1)的条件下,若在第3,4组的志愿者中随机抽取2名志愿者介绍接待外宾经验感受,求第4组至少有1名志愿者被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com