
科目: 来源: 题型:
【题目】过圆![]() 上的点
上的点![]() 作圆
作圆![]() 的切线,过点
的切线,过点![]() 作切线的垂线
作切线的垂线![]() ,若直线
,若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() .
.
(1)求直线![]() 与抛物线
与抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 的准线上,且
的准线上,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市在2017年五一正式开业,开业期间举行开业大酬宾活动,规定:一次购买总额在区间![]() 内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
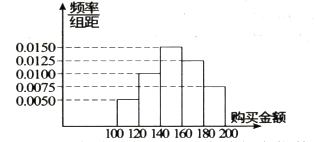
(1)求参与一次抽奖的顾客购买金额的平均数与中位数(同一组中的数据用该组区间的中点值作代表,结果保留到整数);
(2)若根据超市的经营规律,购买金额![]() 与平均利润
与平均利润![]() 有以下四组数据:
有以下四组数据:
![]()
试根据所给数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并根据(1)中计算的结果估计超市对每位顾客所得的利润.
,并根据(1)中计算的结果估计超市对每位顾客所得的利润.
参考公式: 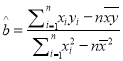 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,
是圆上一动点, ![]() 的垂直平分线与线段
的垂直平分线与线段![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点,并求
过定点,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 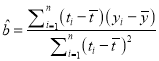 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
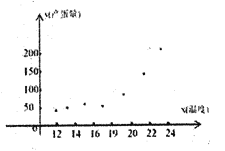
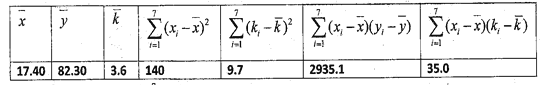
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为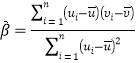 ,
,![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 的正半轴,建立平面直角坐标系
的正半轴,建立平面直角坐标系![]() .
.
(1)若曲线![]() 为参数)与曲线
为参数)与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() ;
;
(2)若![]() 是曲线
是曲线![]() 上的动点,且点
上的动点,且点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com