科目： 来源： 题型：
【题目】如图，四面体ABCD中，△ABC是正三角形，AD=CD．
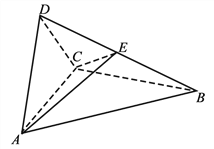
（1）证明：AC⊥BD；
（2）已知△ACD是直角三角形，AB=BD．若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．
查看答案和解析>>
科目： 来源： 题型：
【题目】某销售公司为了解员工的月工资水平，从1000位员工中随机抽取100位员工进行调查，得到如下的频率分布直方图：
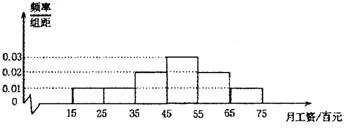
（1）试由此图估计该公司员工的月平均工资；
（2）该公司工资发放是以员工的营销水平为重要依据来确定的，一般认为，工资低于4500。元的员工属于学徒阶段，没有营销经验，若进行营销将会失败;高于4500元的员工是具备营销成熟员工，基进行营销将会成功。现将该样本按照“学徒阶段工资”、“成熟员工工资”分成两层，进行分层抽样，从中抽出5人，在这5人中任选2人进行营销活动。活动中，每位员工若营销成功，将为公司赢得3万元，否则公司将损失1万元。试问在此次比赛中公司收入多少万元的可能性最大？
查看答案和解析>>
科目： 来源： 题型：
【题目】已知向量a＝(sin x，mcos x)，b＝(3，－1).
(1)若a∥b，且m＝1，求2sin2x－3cos2x的值；
(2)若函数f(x)＝a·b的图象关于直线
对称，求函数f(2x)在
上的值域.
查看答案和解析>>
科目： 来源： 题型：
【题目】设函数f(x)＝|2x＋1|＋|x＋1|.
(Ⅰ)求不等式f(x)≤8的解集；
(Ⅱ)若不等式f(x)>|a－2|对任意x∈R恒成立，求实数a的取值范围．
查看答案和解析>>
科目： 来源： 题型：
【题目】以平面直角坐标系的原点为极点，x轴正半轴为极轴建立极坐标系．已知圆C的极坐标方程为ρ＝2sin θ，直线l的参数方程为
(t为参数)，若l与C交于A，B两点．
(Ⅰ)求|AB|；
(Ⅱ)设P(1,2)，求|PA|·|PB|的值．
查看答案和解析>>
科目： 来源： 题型：
【题目】对于函数f(x)(x∈D)，若x∈D时，均有f′(x)<f(x)成立，则称函数f(x)是J函数．
(Ⅰ)当函数f(x)＝x2＋m(ex＋x)，x≥e是J函数时，求实数m的取值范围；
(Ⅱ)若函数g(x)为R＋上的J函数，试比较g(a)与ea－1g(1)的大小．
查看答案和解析>>
科目： 来源： 题型：
【题目】已知椭圆C： 
(a>b>0)的离心率为
，焦距为2c，且c， 
，2成等比数列．
(Ⅰ)求椭圆C的标准方程；
(Ⅱ)点B坐标为(0， 
)，问是否存在过点B的直线l交椭圆C于M，N两点，且满足
(O为坐标原点)？若存在，求出此时直线l的方程；若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】四棱锥A－BCDE中，侧棱AD⊥底面BCDE，底面BCDE是直角梯形，DE∥BC，BC⊥CD，BC＝2AD＝2DC＝2DE＝4，H，I分别是AD，AE的中点．
(Ⅰ)在AB上求作一点F，BC上求作一点G，使得平面FGI∥平面ACD；
(Ⅱ)求平面CHI将四棱锥A－BCDE分成的两部分的体积比．
查看答案和解析>>
科目： 来源： 题型：
【题目】某P2P平台需要了解该平台投资者的大致年龄分布，发现其投资者年龄大多集中在区间[20,50]岁之间，对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查，得到如下统计表和各年龄段人数频率分布直方图：
组数 | 分组 | 人数(单位：人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |
(Ⅰ)求a的值并画出频率分布直方图；
(Ⅱ)在统计表的第五与第六组的5人中，随机选取2人，求这2人的年龄都小于45岁的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com