①f(x)＝2x＋3，x∈R；②f(x)＝x2，x∈；③f(x)＝x2＋1，x∈；④f(x)＝sin x，x∈；⑤f(x)＝log2x，x∈[2，＋∞)．

其中是“定义域上的M函数”的有(　　)

A. 2个 B. 3个

C. 4个 D. 5个

在此几何体中，给出下面四个结论：

①直线BE与直线CF异面； ②直线BE与直线AF异面；

③直线EF∥平面PBC； ④平面BCE⊥平面PAD.

其中正确的有(　　)

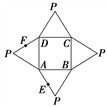
A. 1个 B. 2个 C. 3个 D. 4个

【题目】已知双曲线的焦点是椭圆的顶点， 为椭圆的左焦点且椭圆经过点.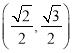

（1）求椭圆的方程；

（2）过椭圆的右顶点作斜率为的直线交椭圆于另一点，连结并延长交椭圆于点，当的面积取得最大值时，求的面积.

【题目】共享单车是指企业的校园，地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是一种分时租赁模式，某共享单车企业为更好服务社会，随机调查了100人，统计了这100人每日平均骑行共享单车的时间（单位：分钟），由统计数据得到如下频率分布直方图，已知骑行时间在三组对应的人数依次成等差数列

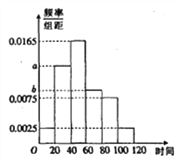
（1）求频率分布直方图中的值.

（2）若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”，将日平均骑行时间少于40分钟的用户为“潜力用户”，现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人，再从这5人中任取3人，求恰好1人为“忠实用户”的概率.

【题目】函数f(x)＝(m2－m－1)·是幂函数，对任意x1，x2∈(0，＋∞)且x1≠x2，满足，若a，b∈R且a＋b>0，ab<0，则f(a)＋f(b)的值(　　)

A. 恒大于0 B. 恒小于0

C. 等于0 D. 无法判断

【题目】给出下列函数：①f(x)＝()x；②f(x)＝x2；③f(x)＝x3；④f(x)＝；⑤f(x)＝log2x.其中满足条件f()>(0<x1<x2)的函数的个数是(　　)

A. 1 B. 2

C. 3 D. 4

【题目】已知椭圆C：，其中（e为椭圆离心率），焦距为2，过点M（4，0）的直线l与椭圆C交于点A，B，点B在AM之间．又点A，B的中点横坐标为．

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）求直线l的方程．

【题目】已知点为抛物线C:的焦点，过点的动直线与抛物线C交于,两点，如图．当直线与轴垂直时，．

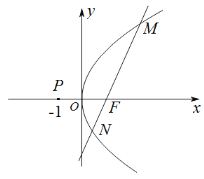
（1）求抛物线C的方程；

（2）已知点,设直线PM的斜率为，直线PN的斜率为．请判断是否为定值，若是，写出这个定值，并证明你的结论；若不是，说明理由．

【题目】已知函数

（1）求曲线在点处的切线方程;

（2）令，讨论的单调性并判断有无极值，若有，求出极值.

【题目】【2018届吉林省普通中学高三第二次调研】设椭圆的左焦点为，右顶点为，离心率为，短轴长为，已知是抛物线的焦点.

（1）求椭圆的方程和抛物线的方程;

（2）若抛物线的准线上两点关于轴对称，直线与椭圆相交于点（异于点），直线与轴相交于点，若的面积为，求直线的方程.