（百台），其总成本为万元（总成本=固定成本+生产成本），并且销售收入满足，假设该产品产销平衡，根据上述统计数据规律求：

（Ⅰ）要使工厂有盈利，产品数量应控制在什么范围？

（Ⅱ）工厂生产多少台产品时盈利最大？

【题目】红星海水养殖场进行某水产品的新旧养殖方法的产量对比，收货时在旧养殖的大量网箱中随机抽取 个网箱，在新养殖法养殖的大量网箱中也随机抽取个网箱，测量各箱水产品的产量，得样本频率分布直方图如下：

（1）填写下列列联表，并根据列联表判断是否有的把握认为箱产量与养殖方法有关.

（2）设两种养殖方法的产量互相独立，记表示事件：“旧养殖法的箱产量低于，新养殖法的箱产量不低于 ”，估计的概率；

（3）某水产批发户从红星海水养殖场用新养殖法养殖的大量网箱水产品中购买了个网箱的水产品，记表示箱产量位于区间的网箱个数，以上样本在相应区间的频率代替概率，求 .

附：

（，其中 ）

【题目】已知函数，

（1）当，时，求函数在上的最小值；

（2）若函数在与处的切线互相垂直，求的取值范围；

（3）设，若函数有两个极值点，，且，求的取值范围．

【题目】如图，已知椭圆与椭圆的离心率相同．

（1）求的值；

（2）过椭圆的左顶点作直线，交椭圆于另一点，交椭圆于两点（点在之间）．①求面积的最大值（为坐标原点）；②设的中点为，椭圆的右顶点为，直线与直线的交点为，试探究点是否在某一条定直线上运动，若是，求出该直线方程；若不是，请说明理由．

【题目】如图，游客从景点下山至有两种路径：一种是从沿直线步行到，另一种是先从乘缆车到，然后从沿直线步行到.现有甲、乙两位游客从下山，甲沿匀速步行，速度为米/分钟.在甲出发分钟后，乙从乘缆车到，在处停留分钟后，再从匀速步行到.已知缆车从到要分钟， 长为米，若，.为使两位游客在处互相等待的时间不超过分钟，则乙步行的速度（米/分钟）的取值范围是 __________．

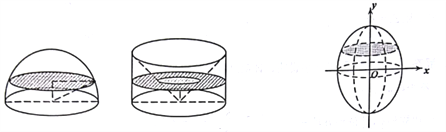
【题目】我国南北朝时间著名数学家祖暅提出了祖暅原理：“幂势既同，则积不容异”.意思是：夹在两平行平面间的两个几何体，被平行于这两个平行平面的任何平面所载，若截得的两个截面面积总相等，则这两个几何体的体积相等.为计算球的体积，构造一个底面半径和高都与球半径相等的圆柱，然后再圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥，运用祖暅原理可证明此几何体与半球体积相等（任何一个平面所载的两个截面面积都相等）.将椭圆 绕 轴旋转一周后得一橄榄状的几何体，类比上述方法，运用祖暅原理可求得其体积等于（ ）

A. B. C. D.

【题目】已知函数 ， ,

⑴ 若有零点，求 m 的取值范围；

⑵ 确定 m 的取值范围，使得有两个相异实根.

【题目】如图，一条小河岸边有相距的两个村庄（村庄视为岸边上两点），在小河另一侧有一集镇（集镇视为点），到岸边的距离为，河宽为，通过测量可知，与的正切值之比为．当地政府为方便村民出行，拟在小河上建一座桥（分别为两岸上的点，且垂直河岸，在的左侧），建桥要求：两村所有人到集镇所走距离之和最短，已知两村的人口数分别是人、人，假设一年中每人去集镇的次数均为次．设．（小河河岸视为两条平行直线）

（1）记为一年中两村所有人到集镇所走距离之和，试用表示；

（2）试确定的余弦值，使得最小，从而符合建桥要求．

(1)求f()的值；

(2)判断y＝f(x)在(0，＋∞)上的单调性并给出证明；

(3)解不等式f(2x)>f(8x－6)－1.

【题目】某超市在节日期间进行有奖促销，凡在该超市购物满元的顾客，将获得一次摸奖机会，规则如下：一个袋子装有只形状和大小均相同的玻璃球，其中两只是红色，三只是绿色，顾客从袋子中一次摸出两只球，若两只球都是红色，则奖励元；共两只球都是绿色，则奖励元；若两只球颜色不同，则不奖励．

（1）求一名顾客在一次摸奖活动中获得元的概率；

（2）记为两名顾客参与该摸奖活动获得的奖励总数额，求随机变量的分布列和数学期望．