
科目: 来源: 题型:
【题目】某煤炭公司销售人员根据该公司以往的销售情况,得到如下频率分布表
日销售量分组 | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
频率 | 0.10 | 0.20 | 0.30 | 0.25 | 0.15 |
(1)在下图中作出这些数据的频率分布直方图;

(2)将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.若未来3天内日销售量不低于6吨的天数为X,求X的分布列、数学期望与方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义在区间D上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ∈D,当
∈D,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数![]() 和
和![]() 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;
(Ⅱ)设![]() 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式![]() 对一切
对一切![]() R恒成立,求实数
R恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,根据性别分层,采用分层抽样的方法从中抽取100名学生进行调查.
(1)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的100名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),如表是根据调查结果得到的![]() 列联表.请将列联表补充完整,并判断是否有
列联表.请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
(2)在抽取到的女生中按(1)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中随机抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
附参考公式及数据: ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
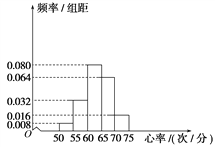
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角为
,倾斜角为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于两点
,且与抛物线交于两点![]() 、
、![]() .
.
(1)求抛物线的标准方程及准线方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的中垂线
的中垂线![]() 交
交![]() 轴于点
轴于点![]() .证明:
.证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
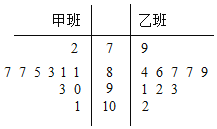
(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知复数z=![]() 2016+(1-i)2(其中i为虚数单位),若复数z的共轭复数为
2016+(1-i)2(其中i为虚数单位),若复数z的共轭复数为![]() ,且
,且![]() ·z1=4+3i.
·z1=4+3i.
(1)求复数z1;
(2)若z1是关于x的方程x2-px+q=0的一个根,求实数p,q的值,并求出方程x2-px+q=0的另一个复数根.
查看答案和解析>>
科目: 来源: 题型:
【题目】某粮食店经销小麦,年销售量为6000千克,每千克小麦进货价为2.8元,销售价为3.4元,全年进货若干次,每次的进货量均为![]() 千克(
千克(![]() ),运费为100元/次,并且全年小麦的总存储费用为
),运费为100元/次,并且全年小麦的总存储费用为![]() 元.
元.
(1)用![]() (千克)表示该粮食店经销小麦的年利润
(千克)表示该粮食店经销小麦的年利润![]() (元);
(元);
(2)每次进货量为多少千克时,能使年利润![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com