
科目: 来源: 题型:
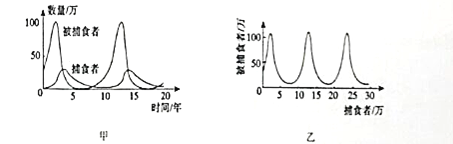
【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是( )
A. 捕食者和被捕食者数量与时间以![]() 年为周期
年为周期
B. 由图可知,当捕食者数量增多的过程中,被捕食者数量先增多后减少
C. 捕食者和被捕食者数量之间的关系可以用图1乙描述
D. 捕食者的数量在第![]() 年和
年和![]() 年之间数量在急速减少
年之间数量在急速减少
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”,“灯者立方去其八角也”,如图所示,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点.
为棱上的四等分点.

(1)求该方灯体的体积;
(2)求直线![]() 和
和![]() 的所成角;
的所成角;
(3)求直线![]() 和平面
和平面![]() 的所成角.
的所成角.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法:
①函数![]() 的单调增区间是
的单调增区间是![]() ;
;
②若函数![]() 定义域为
定义域为![]() 且满足
且满足![]() ,则它的图象关于
,则它的图象关于![]() 轴对称;
轴对称;
③函数![]() 的值域为
的值域为![]() ;
;
④函数![]() 的图象和直线
的图象和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值可能是
的值可能是![]() ;
;
⑤若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中正确的序号是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数:
321 421 292 925 274 632 800 478 598 663 531 297 396
021 506 318 230 113 507 965
据此估计,小张三次射击恰有两次命中十环的概率为()
A. 0.25B. 0.30C. 0.35D. 0.40
查看答案和解析>>
科目: 来源: 题型:
【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”((注)三升九:![]() 升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A.![]() 升B.
升B.![]() 升C.
升C.![]() 升D.
升D.![]() 升
升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com