【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各随机抽取了100件产品作为样本来检测一项质量指标值，若产品的该项质量指标值落在内，则为合格品，否则为不合格品．表1是甲套设备的样本的频数分布表，图是乙套设备的样本的频率分布直方图．

表甲套设备的样本的频数分布表

（1）将频率视为概率．若乙套设备生产了10000件产品，则其中的合格品约有多少件？

（2）填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.01的前提下，认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关．

附表及公式：，其中；

【题目】山西省在2019年3月份的高三适应性考试中对数学成绩数据统计显示，全市10000名学生的成绩近似服从正态分布，现某校随机抽取了50名学生的数学成绩分析，结果这50名学生的成绩全部介于85分到145分之间，现将结果按如下方式分为6组，第一组，第二组，…，第六组，得到如图所示的频率分布直方图：

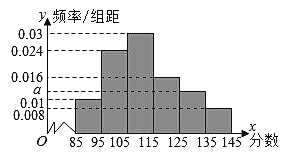
（1）求全市数学成绩在135分以上的人数；

（2）试由样本频率分布直方图佔计该校数学成绩的平均分数；

（3）若从这50名学生中成绩在125分（含125分）以上的同学中任意抽取3人，该3人在全市前13名的人数记为，求的分布列和期望．

附：若，则，，

．

【题目】已知函数， ．

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）若曲线在点处的切线与曲线切于点，求的值；

（Ⅲ）若恒成立，求的最大值．

（1）求选出的4名大学生仅有1名女生的概率；

（2）记选出的4名大学生中女生的人数为，求随机变量的分布列和数学期望.

【题目】各项均为正数的等比数列满足,,若函数的导函数为,则 ( )

A. B. C. D.

【题目】天津大学某学院欲安排4名毕业生到某外资企业的三个部门实习，要求每个部门至少安排1人，其中甲大学生不能安排到部门工作的方法有_______种（用数字作答）.

【题目】已知函数．

（1）求函数的极值；

（2）设函数．若存在区间，使得函数在上的值域为，求实数的取值范围．

【题目】已知椭圆，若在，，，四个点中有3个在上．

（1）求椭圆的方程；

（2）若点与点是椭圆上关于原点对称的两个点，且，求的取值范围．

【题目】某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为小时，其余工人加工完乙型装置所需时间为小时，则生产1000台某产品的总加工时间y是一个关于x的函数。

（1）求y关于x的函数解析式；

（2）如何分配工人才能使生产1000台某产品的总加工时间最少？

【题目】某高校通过自主招生方式在贵阳招收一名优秀的高三毕业生，经过层层筛选，甲、乙两名学生进入最后测试，该校设计了一个测试方案：甲、乙两名学生各自从6个问题中随机抽3个问题．已知这6道问题中，学生甲能正确回答其中的4个问题，而学生乙能正确回答每个问题的概率均为，甲、乙两名学生对每个问题的回答都是相互独立、互不影响的．

（1）求甲、乙两名学生共答对2个问题的概率．

（2）请从期望和方差的角度分析，甲、乙两名学生哪位被录取的可能性更大？