
科目: 来源: 题型:
【题目】《中国诗词大会》节目组决定把《将进酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》与《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,且均不排在最后,则后六场开场诗词的排法有_____________种.(用数字作答)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
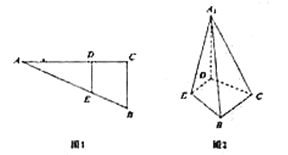
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 长为多少时,异面直线
长为多少时,异面直线![]() ,
,![]() 所成的角最小,并求出此时所成角的余弦值.
所成的角最小,并求出此时所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求![]() 的估计值;
的估计值;
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A. 若直线a,b与平面α所成角都是30°,则这两条直线平行
B. 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C. 若直线a,b平行,则这两条直线中至少有一条与平面α平行
D. 若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目: 来源: 题型:
【题目】关于函数 ,下列判断正确的是( )
,下列判断正确的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的图象的对称中心为
的图象的对称中心为![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在单调递减区间
上存在单调递减区间
D. ![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位而得
个单位而得
查看答案和解析>>
科目: 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是 ( )
2017 2016 2015 2014……6 5 4 3 2 1
4033 4031 4029…………11 9 7 5 3
8064 8060………………20 16 12 8
16124……………………36 28 20
………………………
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
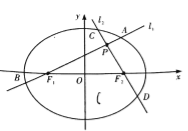
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 为
为![]() 的下标.如果数组
的下标.如果数组![]() 中的每个“元”都来自数组
中的每个“元”都来自数组![]() 中不同下标的“元”则称
中不同下标的“元”则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值及此时的数组
的最大值及此时的数组![]() ;
;
(2)若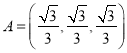 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com