
科目: 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 的三等分点(如图1).将
的三等分点(如图1).将![]() 沿着
沿着![]() 折起到
折起到![]() 的位置,连接
的位置,连接![]() (如图2).
(如图2).

(1)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(2)记线段![]() 的中点为
的中点为![]() ,平面
,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目: 来源: 题型:
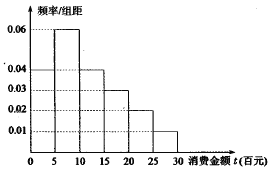
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的中位数
的中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
(3)将(2)中的频率当作概率,电子商务平台从该市网民中随机抽取10人赠送电子礼金,求这10人中女性的人数![]() 的数学期望.
的数学期望.
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
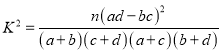 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() ,动点
,动点![]() 到点
到点![]() 的距离比点
的距离比点![]() 到
到![]() 的距离小1.
的距离小1.
(1)求动点P的轨迹C的方程;
(2)过点![]() 的直线
的直线![]() 与(1)中轨迹C相交于两个不同的点M、N,若
与(1)中轨迹C相交于两个不同的点M、N,若![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为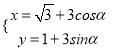 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的一条直角是椭圆
的一条直角是椭圆![]() 的长轴,动直线
的长轴,动直线![]() ,当
,当![]() 过椭圆
过椭圆![]() 上一点
上一点![]() 且与圆
且与圆![]() 相交于点
相交于点![]() 时,弦
时,弦![]() 的最小值为
的最小值为![]() .
.
(1)求圆即椭圆![]() 的方程;
的方程;
(2)若直线![]() 是椭圆
是椭圆![]() 的一条切线,
的一条切线,![]() 是切线上两个点,其横坐标分别为
是切线上两个点,其横坐标分别为![]() ,那么以
,那么以![]() 为直径的圆是否经过
为直径的圆是否经过![]() 轴上的定点?如果存在,求出定点坐标;若不存在,请说明理由.
轴上的定点?如果存在,求出定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈[14,40]时,曲线是函数![]() (
(![]() 且
且![]() )图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲完?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com