
科目: 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为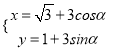 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的一条直径是椭圆
的一条直径是椭圆![]() 的长轴,过椭圆
的长轴,过椭圆![]() 上一点
上一点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于点
相交于点![]() ,弦
,弦![]() 的最小值为
的最小值为![]() .
.
(1)求圆![]() 及椭圆
及椭圆![]() 的方程;
的方程;
(2) 已知点![]() 是椭圆
是椭圆![]() 上的任意一点,点
上的任意一点,点![]() 是
是![]() 轴上的一定点,直线
轴上的一定点,直线![]() 的方程为
的方程为![]() ,若点
,若点![]() 到定直线
到定直线![]() 的距离与到定点
的距离与到定点![]() 的距离之比为
的距离之比为![]() ,求定点
,求定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】两人约定在20∶00到21∶00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20∶00至21∶00各时刻相见的可能性是相等的,则他们两人在约定时间内相见的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年
年![]() 月某城市国际马拉松赛正式举行,组委会对
月某城市国际马拉松赛正式举行,组委会对![]() 名裁判人员进(年龄均在
名裁判人员进(年龄均在![]() 岁到
岁到![]() 岁)行业务培训,现按年龄(单位:岁)进行分组统计:第
岁)行业务培训,现按年龄(单位:岁)进行分组统计:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如下:
,得到的频率分布直方图如下:
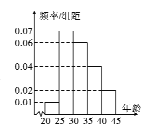
(1)若把这![]() 名裁判人员中年龄在
名裁判人员中年龄在![]() 称为青年组,其中男裁判
称为青年组,其中男裁判![]() 名;年龄在
名;年龄在![]() 的称为中年组,其中男裁判
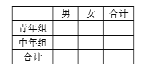
的称为中年组,其中男裁判![]() 名.试完成
名.试完成![]() 列联表并判断能否在犯错误的概率不超过
列联表并判断能否在犯错误的概率不超过![]() 的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
(2)培训前组委会用分层抽样调查方式在第![]() 组共抽取了
组共抽取了![]() 名裁判人员进行座谈,若将其中抽取的第
名裁判人员进行座谈,若将其中抽取的第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,若组委会决定从上述
,若组委会决定从上述![]() 名裁判人员中再随机选
名裁判人员中再随机选![]() 人参加新闻发布会,要求这
人参加新闻发布会,要求这![]() 组各选
组各选![]() 人,试求裁判人员
人,试求裁判人员![]() 不同时被选择的概率;
不同时被选择的概率;
附: 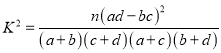
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com