
科目: 来源: 题型:
【题目】某市创业园区新引进一家生产环保产品的公司,已知该环保产品每售出1盒的利润为0.3万元,当月未售出的环保产品,每盒亏损0.12万元.根据统计资料,该环保产品的市场月需求量的频率分布直方图如图所示.
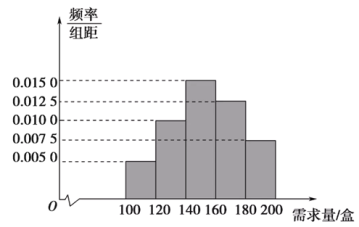
(1)若该环保产品的月进货量为160盒,以![]() (单位:盒,
(单位:盒,![]() )表示该产品一个月内的市场需求量,
)表示该产品一个月内的市场需求量,![]() (单位:万元)表示该公司生产该环保产品的月利润.
(单位:万元)表示该公司生产该环保产品的月利润.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②根据频率分布直方图估计利润![]() 不少于39.6万元的概率.
不少于39.6万元的概率.
(2)在频率分布直方图的月需求量分组中,以各组的区间中点值代表该组的月需求量,当月进货量为158箱时,写出月利润![]() (单位:万元)的所有可能值.
(单位:万元)的所有可能值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程:
的直角坐标方程:
(Ⅱ)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目: 来源: 题型:
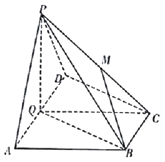
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为振兴旅游业,香港计划向内陆地区发行总量为2000万张的紫荆卡,其中向内陆人士(广东户籍除外)发行的是紫荆金卡(简称金卡),向广东籍人士发行的是紫荆银卡(简称银卡).某旅游公司组织了一个有36名内陆游客的旅游团到香港名胜旅游,其中![]() 是非广东籍内陆游客,其余是广东籍游客.在非广东新游客中有
是非广东籍内陆游客,其余是广东籍游客.在非广东新游客中有![]() 持金卡,在广东籍游客中有
持金卡,在广东籍游客中有![]() 持银卡.
持银卡.
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的广东籍游客中随机采访3名游客,设其中持银卡人数为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】先后2次抛掷一次骰子,将得到的点数分别记为![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某鲜奶店每天以每瓶3元的价格从牧场购进若干瓶鲜牛奶,然后以每瓶7元的价格出售.如果当天卖不完,剩下的鲜牛奶作垃圾处理.
(1)若鲜奶店一天购进30瓶鲜牛奶,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:瓶,
(单位:瓶,![]() )的函数解析式;
)的函数解析式;
(2)鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶),绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5):
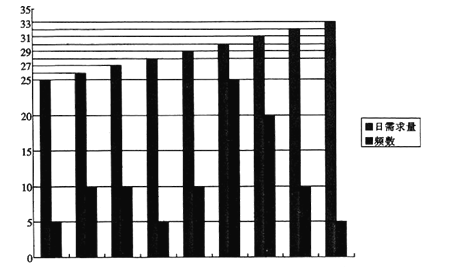
以100天记录的各需求量的频率作为各需求量发生的概率.
(ⅰ)若该鲜奶店一天购进30瓶鲜奶,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ⅱ)若该鲜奶店计划一天购进29瓶或30瓶鲜牛奶,你认为应购进29瓶还是30瓶?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某省为了确定合理的阶梯电价分档方案,对全省居民用量进行了一次抽样调查,得到居民月用电量(单位:度)的频率分布直方图(如图所示),求:
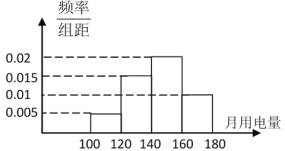
(1)若要求80%的居民能按基本档的电量收费,则基本档的月用电量应定为多少度?
(2)由频率分布直方图可估计,居民月用电量的众数、中位数和平均数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com