
科目: 来源: 题型:
【题目】为落实国家“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2017年在其扶贫基地投入100万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上,每年投入的资金比上一年增长![]() .
.
(1)写出第![]() 年(2018年为第一年)该企业投入的资金数
年(2018年为第一年)该企业投入的资金数![]() (万元)与
(万元)与![]() 的函数关系式,并指出函数的定义域
的函数关系式,并指出函数的定义域
(2)该企业从第几年开始(2018年为第一年),每年投入的资金数将超过200万元?(参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某省级示范高中高三年级对考试的评价指标中,有“难度系数”和“区分度”两个指标.其中,难度系数=年级总平均分![]() 总分,区分度=(实验班的平均分—普通班的平均分)
总分,区分度=(实验班的平均分—普通班的平均分)![]() 总分.
总分.
(1)某次数学考试满分150分,随机从实验班和普通班各抽取三人,实验班三人的成绩分别为:147、142、137;普通班三人的成绩分别为:97、102、113,通过样本计算本次考试的区分度(精确到0.01);
(2)以下表格是高三年级6次考试的统计数据:

令![]() ,求出
,求出![]() 关于
关于![]() 的线性回归方程,并预报
的线性回归方程,并预报![]() 时
时![]() 的值(系数精确到0.01).
的值(系数精确到0.01).
参考数据:![]() ,
,![]() .
.
回归方程中斜率和截距的最小二乘法公式分别为: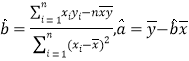 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一微商店对某种产品每天的销售量(![]() 件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.
件)进行为期一个月的数据统计分析,并得出了该月销售量的直方图(一个月按30天计算)如图所示.假设用直方图中所得的频率来估计相应事件发生的概率.

(1)求频率分布直方图中![]() 的值;
的值;
(2)求日销量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若微商在一天的销售量超过25件(包括25件),则上级商企会给微商赠送100元的礼金,估计该微商在一年内获得的礼金数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)证明: ![]() ;
;
(Ⅱ)若棱锥![]() 的体积为
的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】【试题分析】(I) 取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .利用等腰三角形的性质和矩形的性质可证得
.利用等腰三角形的性质和矩形的性质可证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,故
,故![]() ,故
,故![]() .(II) 可知
.(II) 可知![]() 是棱锥的高,利用体积公式求得
是棱锥的高,利用体积公式求得![]() ,利用勾股定理和等腰三角形的性质求得
,利用勾股定理和等腰三角形的性质求得![]() 的值,进而求得面积.
的值,进而求得面积.
【试题解析】
证明:(Ⅰ)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,∴
为矩形,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,所以
,所以![]() .
.
(Ⅱ)由面![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,所以
,所以![]() 为棱锥
为棱锥![]() 的高,
的高,
由![]() ,知
,知![]() ,
,
![]()
![]()
![]() ,
,
∴![]() .
.
由(Ⅰ)知![]() ,
,![]() ,∴
,∴![]() .
.
![]() .
.
由![]() ,可知
,可知![]() 平面
平面![]() ,∴
,∴![]() ,
,
因此![]() .
.
在![]() 中
中![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]() .
.
所以棱锥![]() 的侧面积为
的侧面积为![]() .
.
【题型】解答题
【结束】
20
【题目】已知圆![]() 经过椭圆
经过椭圆![]() :
: ![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,它们在
上的两点,它们在![]() 轴两侧,且
轴两侧,且![]() 的平分线在
的平分线在![]() 轴上,
轴上, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三统考结束后,分别从喜欢数学和不喜欢数学的学生中各随机抽取了10人的成绩,分数都是整数,得到如下茎叶图,但是喜欢数学和不喜欢数学的各缺失了一个数据.若已知不喜欢数学的10人成绩的中位数为75,且已知喜欢数学的10人中所缺失成绩是85分以上,但是不高于喜欢数学的10人的平均分.不喜欢数学和喜欢数学缺失的数据分别是____,____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com