
科目: 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点,将四边形
的中点,将四边形![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,如图2所示,
,如图2所示,![]() 是
是![]() 上一点,且
上一点,且![]() .
.

(1)求证:![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与抛物线的准线相切.
过原点且与抛物线的准线相切.
(1)求该抛物线的方程;
(2)过抛物线焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
, ![]() 两点,分别在点
两点,分别在点![]() ,
, ![]() 处作抛物线的两条切线交于
处作抛物线的两条切线交于![]() 点,求三角形
点,求三角形![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
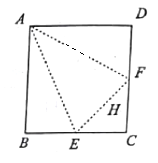
【题目】如图,在边长为2的正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将正方形折起,使
将正方形折起,使![]() 重合于点
重合于点![]() ,在构成的四面体
,在构成的四面体![]() 中,下列结论错误的是
中,下列结论错误的是
A. ![]() 平面
平面![]()
B. 直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]()
C. 四面体![]() 的内切球表面积为
的内切球表面积为![]()
D. 异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某产品生产厂家根据以往销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为g(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足![]() 假设该产品产销平衡,试根据上述资料
假设该产品产销平衡,试根据上述资料
(Ⅰ)要使工厂有盈利,产量x应控制在什么范围内;
(Ⅱ)工厂生产多少台产品时,可使盈利最多?
(Ⅲ)当盈利最多时,求每台产品的售价.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据绘制的散点图能够看出可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明;(系数精确到0.001)
加以说明;(系数精确到0.001)
(2)建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
(系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:(1)样本![]() 的相关系数
的相关系数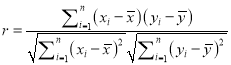
(2)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为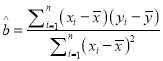 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校![]() 、
、![]() 两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下,通过茎叶图比较两班数学兴趣小组成绩的平均值及方差
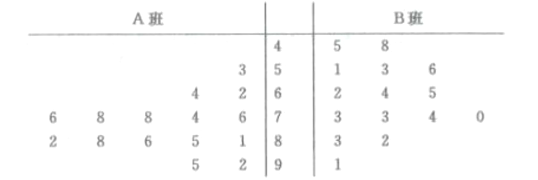
①![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
②![]() 班数学兴趣小组的平均成绩高于
班数学兴趣小组的平均成绩高于![]() 班的平均成绩
班的平均成绩
③![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
④![]() 班数学兴趣小组成绩的标准差大于
班数学兴趣小组成绩的标准差大于![]() 班成绩的标准差
班成绩的标准差
其中正确结论的编号为( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-![]() ,0),B(
,0),B(![]() ,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为
,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为![]() ,设动点M的轨迹为曲线E.
,设动点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)过曲线E外一点Q作E的两条切线l1,l2,若它们的斜率之积为-1,那么![]() ·
·![]() 是否为定值?若是,请求出该值;若不是,请说明理由.
是否为定值?若是,请求出该值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() )
)
(1)判断并证明![]() 的奇偶性;
的奇偶性;
(2)求使![]() 的
的![]() 的取值范围;
的取值范围;
(3)若
![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 有三个不同的零点,若存在,求出
有三个不同的零点,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com