
科目: 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别是240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动。
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作,求事件M“抽取的2名同学来自同一年级”发生的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 且与
且与![]() 轴不重合的直线
轴不重合的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(ⅰ)求![]() 的方程;
的方程;
(ⅱ)记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是![]() 和an的等差中项.
和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=-n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划在办公大厅建一面长为![]() 米的玻璃幕墙.先等距安装
米的玻璃幕墙.先等距安装![]() 根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为
根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为![]() 米的玻璃造价为
米的玻璃造价为![]() 元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为
元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为![]() 元(总造价=立柱造价+玻璃造价).
元(总造价=立柱造价+玻璃造价).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,怎样设计能使总造价最低?
时,怎样设计能使总造价最低?
查看答案和解析>>
科目: 来源: 题型:
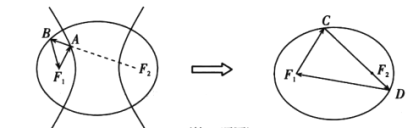
【题目】光线从椭圆的一个焦点发出,被椭圆反射后会经过椭圆的另一个焦点;光线从双曲线的一个焦点发出,被双曲线反射后的反射光线等效于从另一个焦点射出.如图,一个光学装置由有公共焦点![]() ,
,![]() 的椭圆
的椭圆![]() 与双曲线
与双曲线![]() 构成,现一光线从左焦点
构成,现一光线从左焦点![]() 发出,依次经
发出,依次经![]() 与
与![]() 反射,又回到了点
反射,又回到了点![]() ,历时
,历时![]() 秒;若将装置中的
秒;若将装置中的![]() 去掉,此光线从点
去掉,此光线从点![]() 发出,经
发出,经![]() 两次反射后又回到了点
两次反射后又回到了点![]() ,历时
,历时![]() 秒;若
秒;若![]() ,则
,则![]() 与
与![]() 的离心率之比为( )
的离心率之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足:an+1-an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=![]() ,bn+1-bn=2an,求数列{bn}的通项公式.
,bn+1-bn=2an,求数列{bn}的通项公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”
之间为“体质不合格”![]() 现从两个年级中各随机抽取8名学生,测试成绩如下:
现从两个年级中各随机抽取8名学生,测试成绩如下:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a,b是正整数.
(1)若该校高一年级有200名学生,试估计高一年级“体质优秀”的学生人数;
(2)从高一年级抽取的学生中再随机选取3人,求这3人中,恰有1人“体质良好”的概率;
(3)设两个年级被抽取学生的测试成绩的平均数相等,当高二年被抽取学生的测试成绩的方差最小时,写出a,b的值![]() 结论不要求证明
结论不要求证明![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)在(-∞,+∞)上有意义,且对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|并且函数f(x+1)的对称中心是(-1,0),若函数g(x)-f(x)=x,则不等式g(2x-x2)+g(x-2)<0的解集是( ).
A.![]() B.
B.![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,侧棱
中,底面ABCD为正方形,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,E,F,H分别是线段PA,PD,AB的中点.
,E,F,H分别是线段PA,PD,AB的中点.
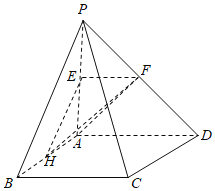
(1)求证:![]() 平面EFH;
平面EFH;
(2)求证:![]() 平面AHF;
平面AHF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com