
科目: 来源: 题型:
【题目】下列说法中错误的为![]()
A.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]()
B.向量![]() ,
,![]() 不能作为平面内所有向量的一组基底
不能作为平面内所有向量的一组基底
C.若![]() ,则
,则![]() 在
在![]() 方向上的正射影的数量为
方向上的正射影的数量为![]()
D.三个不共线的向量![]() ,
,![]() ,
,![]() ,满足
,满足
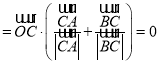 ,则
,则![]() 是
是![]() 的内心
的内心
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司准备将![]() 万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润
万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
|
|
|
|
|
|
|
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整的次数
.若乙项目产品价格一年内调整的次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
|
|
|
|
|
|
|
|
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的分布列;
的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx![]() x2,g(x)
x2,g(x)![]() x2+x,m∈R,令F(x)=f(x)+g(x).
x2+x,m∈R,令F(x)=f(x)+g(x).
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;
(Ⅲ)若m=﹣1,且正实数x1,x2满足F(x1)=﹣F(x2),求证:x1+x2![]() 1.
1.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2ex﹣b,其中b∈R.
(Ⅰ)证明:对于任意x1,x2∈(﹣∞,0],都有f(x1)﹣f(x2)![]() ;
;
(Ⅱ)讨论函数f(x)的零点个数(结论不需要证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2lnx﹣x.
(I)写出函数f(x)的定义域,并求其单调区间;
(II)已知曲线y=f(x)在点(x0,f(x0))处的切线为l,且l在y轴上的截距是﹣2,求x0.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义域为[0,1]的函数f(x)同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0;
②f(1)=1;
③当x1,x2∈[0,1],且x1+x2∈[0,1]时,f(x1+x2)≥f(x1)+f(x2)成立.称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知f(x)为“友谊函数”,求f(0)的值;
(2)函数g(x)=2x-1在区间[0,1]上是否为“友谊函数”?请给出理由;
(3)已知f(x)为“友谊函数”,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,求证: f(x0)=x0.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() ∶
∶![]() 和圆
和圆![]() ∶
∶![]() ,
,![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)若![]() ,求点
,求点![]() 坐标;
坐标;
(2)若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)设线段![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com