
【题目】下列说法中错误的为![]()
A.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]()
B.向量![]() ,
,![]() 不能作为平面内所有向量的一组基底
不能作为平面内所有向量的一组基底
C.若![]() ,则
,则![]() 在
在![]() 方向上的正射影的数量为
方向上的正射影的数量为![]()
D.三个不共线的向量![]() ,
,![]() ,
,![]() ,满足
,满足
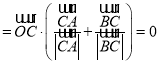 ,则
,则![]() 是
是![]() 的内心
的内心
【答案】AC
【解析】
对于A,由向量的交角为锐角的等价条件为数量积大于0,且两向量不共线,计算即可;
对于B,由![]() ,可知
,可知![]() ,
,![]() 不能作为平面内所有向量的一组基底;
不能作为平面内所有向量的一组基底;
对于C,利用向量投影的定义即可判断;
对于D,由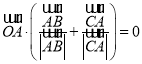 ,点
,点![]() 在角
在角![]() 的平分线上,同理,点
的平分线上,同理,点![]() 在角
在角![]() 的平分线上,点
的平分线上,点![]() 在角
在角![]() 的平分线上,进而得出点
的平分线上,进而得出点![]() 是
是![]() 的内心.
的内心.
对于A,已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,
的夹角为锐角,
可得![]() ,且
,且![]() 与
与![]() 不共线,
不共线,![]() ,
,
即有![]() ,且
,且![]() ,
,
解得![]() 且
且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() 且
且![]() ,
,
故A不正确;
对于B,向量,,![]() ,
,
![]()
![]() ,
,
![]() 向量
向量![]() ,
,![]() 不能作为平面内所有向量的一组基底,故B正确;
不能作为平面内所有向量的一组基底,故B正确;
对于C,若![]() ,则
,则![]() 在
在![]() 上的投影为
上的投影为![]() ,故C错误;
,故C错误;
对于D,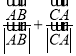 表示与
表示与![]() 中角
中角![]() 的外角平分线共线的向量,
的外角平分线共线的向量,
由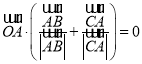 ,可知
,可知![]() 垂直于角
垂直于角![]() 的外角平分线,
的外角平分线,
所以,点![]() 在角
在角![]() 的平分线上,
的平分线上,
同理,点![]() 在角
在角![]() 的平分线上,点
的平分线上,点![]() 在角
在角![]() 的平分线上,
的平分线上,
故点![]() 是
是![]() 的内心,D正确.
的内心,D正确.
故选:AC.


科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
![]() 1
1![]() 求圆C的普通方程和直线l的直角坐标方程;
求圆C的普通方程和直线l的直角坐标方程;
![]() 2
2![]() 设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

则参加测试的总人数为______,分数在![]() 之间的人数为______.
之间的人数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com