
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 与
与![]() 的公共点为
的公共点为![]() ,且
,且![]() 是曲线
是曲线![]() 的中心,求
的中心,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() 在同一个周期内,当
在同一个周期内,当![]() 时y取最大值1,当
时y取最大值1,当![]() 时,y取最小值﹣1.
时,y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)函数y=sinx的图象经过怎样的变换可得到y=f(x)的图象?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
查看答案和解析>>
科目: 来源: 题型:
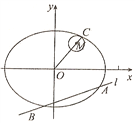
【题目】如图所示,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心在原点,点
的中心在原点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 上一点,圆
上一点,圆![]() 的半径为
的半径为![]() ,且
,且![]() ,求
,求![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
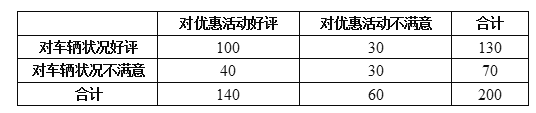
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.
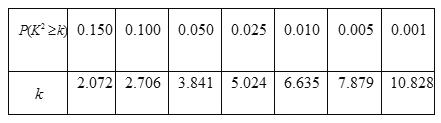
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】207年8月8日晚我国四川九赛沟县发生了7.0级地震,为了解与掌握一些基本的地震安全防护知识,某小学在9月份开学初对全校学生进行了为期一周的知识讲座,事后并进行了测试(满分100分),根据测试成绩评定为“合格”(60分以上包含60分)、“不合格”两个等级,同时对相应等级进行量化:“合格”定为10分,“不合格”定为5分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
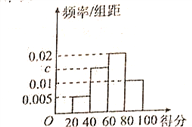
(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈,现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)设函数![]() (其中
(其中![]() 表示
表示![]() 的方差)是评估安全教育方案成效的一种模拟函数.当
的方差)是评估安全教育方案成效的一种模拟函数.当![]() 时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
参考公式及数据: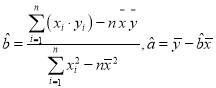
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com