
科目: 来源: 题型:
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)在阅读量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人的成绩优秀,在阅量为
人的成绩优秀,在阅量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人成绩不优秀,请完成下面的
人成绩不优秀,请完成下面的![]() 列联表,并判断在“犯错误概率不超过
列联表,并判断在“犯错误概率不超过![]() ”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
阅读量为 | 阅读量为 | 合计 | |
成绩优秀的人数 | |||
成绩不优秀的人数 | |||
合计 |
(2)在抽出的同学中,1)求抽到被污染部分的同学人数;2)从阅读量在![]() 万到
万到![]() 万字及
万字及![]() 万到
万到![]() 万字的同学中选出
万字的同学中选出![]() 人写出阅读的心得体会.求这
人写出阅读的心得体会.求这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,
, ![]() ,
, ![]() 是其长轴顶点,
是其长轴顶点, ![]() 是椭圆上异于
是椭圆上异于![]() ,
, ![]() 的动点,且
的动点,且![]() .
.
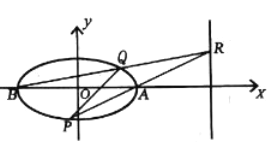
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,若动点![]() 在直线
在直线![]() 上,直线
上,直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
, ![]() 两点.请问:直线
两点.请问:直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市为调查会员某年度上半年的消费情况制作了有奖调查问卷发放给所有会员,并从参与调查的会员中随机抽取![]() 名了解情况并给予物质奖励.调查发现抽取的
名了解情况并给予物质奖励.调查发现抽取的![]() 名会员消费金额(单位:万元)都在区间
名会员消费金额(单位:万元)都在区间![]() 内,调查结果按消费金额分成
内,调查结果按消费金额分成![]() 组,制作成如下的频率分布直方图.
组,制作成如下的频率分布直方图.

(1)求该![]() 名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
(2)若再从这![]() 名会员中选出一名会员参加幸运大抽奖,幸运大抽奖方案如下:会员最多有两次抽奖机会,每次抽奖的中奖概率均为
名会员中选出一名会员参加幸运大抽奖,幸运大抽奖方案如下:会员最多有两次抽奖机会,每次抽奖的中奖概率均为![]() ,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则会员获得
,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则会员获得![]() 元奖金,不进行第二次抽奖;若正面朝上,会员需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金
元奖金,不进行第二次抽奖;若正面朝上,会员需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金![]() 元,如果未中奖,则所获得的奖金为
元,如果未中奖,则所获得的奖金为![]() 元.若参加幸运大抽奖的会员所获奖金(单位:元)用
元.若参加幸运大抽奖的会员所获奖金(单位:元)用![]() 表示,求
表示,求![]() 的分布列与期望值
的分布列与期望值![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 图象上最高点与该最高点相邻的图象的对称中心的距离为
图象上最高点与该最高点相邻的图象的对称中心的距离为![]() .
.
(1)求函数![]() 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)把![]() 图象上所有的点先横坐标伸长为原来的
图象上所有的点先横坐标伸长为原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位得到函数
个单位得到函数![]() 的图象.在
的图象.在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别是角
分别是角![]() ,
, ![]() ,
, ![]() 的对边,若
的对边,若![]() ,
, ![]() 的面积为
的面积为![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,求
成等差数列,求![]() 的周长.
的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 | PM2.5平均浓度 | 频数 | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com