
科目: 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.

若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目: 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)求三棱锥![]() 的体积的最大值.
的体积的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一个表面被涂上红色的棱长是4cm的立方体,将其适当分割成棱长为1cm的小立方体.

(1)共得到多少个棱长是1cm的小立方体?
(2)三面是红色的小立方体有多少个?它们的表面积之和是多少?
(3)两面是红色的小立方体有多少个?它们的表面积之和是多少?
(4)一面是红色的小立方体有多少个?它们的表面积之和是多少?
(5)六个面均没有颜色的小立方体有多少个?它们的表面积之和是多少?它们占有多少立方厘米的空间?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足;对任意
,如果满足;对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若![]() 是
是![]() 上的有界函数,且
上的有界函数,且![]() 的上界为3,求实数
的上界为3,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求函数
,求函数![]() 在
在![]() 上的上界
上的上界![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知一圆台上底面的半径为2,下底面的半径为3,截得此圆台的圆锥的高为6,则此圆台的体积为________.
(2)圆台的上、下底面半径分别为10cm,20cm,它的侧面展开图扇环的圆心角为180°,则圆台的表面积为______![]() .(结果中保留π)
.(结果中保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.
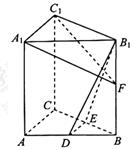
求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 是函数
是函数![]() 的反函数.
的反函数.
![]() 求函数
求函数![]() 的解析式,并写出定义域
的解析式,并写出定义域![]() ;
;
![]() 设
设![]() ,判断并证明函数
,判断并证明函数![]() 在区间
在区间![]() 上的单调性:
上的单调性:
![]() 若
若![]() 中的函数
中的函数![]() 在区间
在区间![]() 内的图像是不间断的光滑曲线,求证:函数
内的图像是不间断的光滑曲线,求证:函数![]() 在区间
在区间![]() 内必有唯一的零点(假设为
内必有唯一的零点(假设为![]() ),且
),且![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com