在平面直角坐标系中，曲线的参数方程为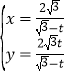（为参数，且），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为.

（1）将曲线的参数方程化为普通方程，并将曲线的极坐标方程化为直角坐标方程；

（2）求曲线与曲线交点的极坐标.

【题目】已知双曲线与有相同的渐近线，且经过点，

（1）求双曲线的方程，并写出其离心率与渐近线方程；

（2）已知直线与双曲线交于不同的两点，且线段的中点在圆上，求实数的取值.

【题目】已知二次函数满足：①，有；②；③的图像与x轴两交点间距离为4．

（1）求的解析式；

（2）记，．

①若为单调函数，求k的取值范围；

②记的最小值为，讨论的零点个数．

【题目】根据以往的经验，某建筑工程施工期间的降水量（单位：）对工期的影响如下表：

根据某气象站的资料，某调查小组抄录了该工程施工地某月前20天的降水量的数据，绘制得到降水量的折线图，如下图所示.

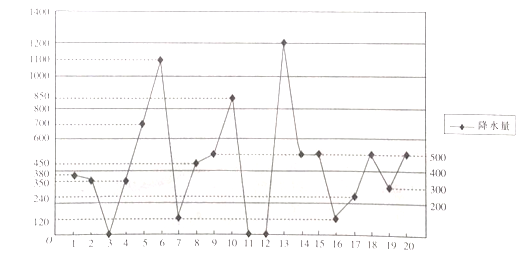
（1）求这20天的平均降水量；

（2）根据降水量的折线图，分别估计该工程施工延误天数的概率.

（1）求异面直线AB和CD所成的角的大小；

（2）求证：直线a∥α且CN＝DN．

（1）求抛物线C的方程；

（2）求线段MN的长．

A. 6种 B. 8种 C. 10种 D. 12种

A. 是偶数?，? B. 是奇数?，?

C. 是偶数?， ? D. 是奇数?，?

（1）求图中的值；

（2）根据已知条件完成下面列联表，并判断能否有的把握认为“晋级成功”与性别有关？

（3）将频率视为概率，从本次考试的所有人员中，随机抽取4人进行约谈，记这4人中晋级失败的人数为，求的分布列与数学期望．

（参考公式：，其中）

【题目】某森林出现火灾，火势正以每分钟的速度顺风蔓延，消防站接到警报立即派消防队员前去，在火灾发生后分钟到达救火现场，已知消防队员在现场平均每人每分钟灭火，所消耗的灭火材料、劳务津贴等费用为每人每分钟125元，另附加每次救火所损耗的车辆、器械和装备等费用平均每人100元，而烧毁一平方米森林损失费为60元.

（1）设派名消防队员前去救火，用分钟将火扑灭，试建立与的函数关系式；

（2）问应该派多少名消防队员前去救火，才能使总损失最少？

（总损失=灭火材料、劳务津贴等费用+车辆、器械和装备费用+森林损失费）