
科目: 来源: 题型:
【题目】如图,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,垂足为N , AE⊥PB,垂足为E .
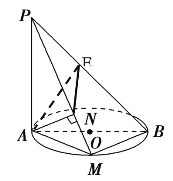
(1)求证:平面PAM⊥平面PBM.
(2)求证:![]() 是二面角A-PB-M的平面角.
是二面角A-PB-M的平面角.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知矩形的面积为100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
(2)已知矩形的周长为36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2016·郑州模拟)某市公安局为加强安保工作,特举行安保项目的选拔比赛活动,其中A、B两个代表队进行对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式进行三场比赛,每场胜队得1分,负队得0分,设A队、B队最后所得总分分别为ξ,η,且ξ+η=3.
对阵队员 | A队队员胜 | A队队员负 |
A1对B1 |
|
|
A2对B2 |
|
|
A3对B3 |
|
|
(1)求A队最后所得总分为1的概率;
(2)求ξ的分布列,并用统计学的知识说明哪个队实力较强.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
,![]() 处切线的斜率分别是
处切线的斜率分别是![]() ,
,![]() 规定
规定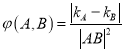 (
(![]() 为线段
为线段![]() 的长度)叫做曲线
的长度)叫做曲线![]() 在点
在点![]() 与
与![]() 之间的“平方弯曲度”,给出以下命题:
之间的“平方弯曲度”,给出以下命题:
①函数![]() 图象上两点
图象上两点![]() 与
与![]() 的横坐标分别为1和2,则
的横坐标分别为1和2,则![]() ;
;
②存在这样的函数,图象上任意两点之间的“平方弯曲度”为常数;
③设点![]() ,
,![]() 是抛物线
是抛物线![]() 上不同的两点,则
上不同的两点,则![]() ;
;
④设曲线![]() (
(![]() 是自然对数的底数)上不同两点
是自然对数的底数)上不同两点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最大值为
的最大值为![]() .
.
其中真命题的序号为__________(将所有真命题的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一2班学生每周用于数学学习的时间![]() (单位:
(单位:![]() )与数学成绩
)与数学成绩![]() (单位:分)之间有如下数据:
(单位:分)之间有如下数据:
| 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
查看答案和解析>>
科目: 来源: 题型:
【题目】(题文)某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ,求随机变量ξ的分布列和均值E(ξ).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,圆心
,圆心![]() 在
在![]() 轴上.
轴上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com