
科目: 来源: 题型:
【题目】某餐厅经营盒饭生意,每天的房租、人员工资等固定成本为200元,每盒盒饭的成本为15元,销售单价与日均销售量的关系如下表

根据以上数据,当这个餐厅每盒盒饭定价______元时,利润最大
A.16.5B.19.5C.21.5D.22
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,其外接圆为
,其外接圆为![]() .对于线段
.对于线段![]() 上的任意一点
上的任意一点![]() ,
,
若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,则
的中点,则![]() 的半径
的半径![]() 的取值范围__________.
的取值范围__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,OB、CD是两条互相平行的笔直公路,且均与笔直公路OC垂直(公路宽度忽略不计),半径OC=1千米的扇形COA为该市某一景点区域,当地政府为缓解景点周边的交通压力,欲在圆弧AC上新增一个入口E(点E不与A、C重合),并在E点建一段与圆弧相切(E为切点)的笔直公路与OB、CD分别交于M、N.当公路建成后,计划将所围成的区域在景点之外的部分建成停车场(图中阴影部分),设∠CON=θ,停车场面积为S平方千米.
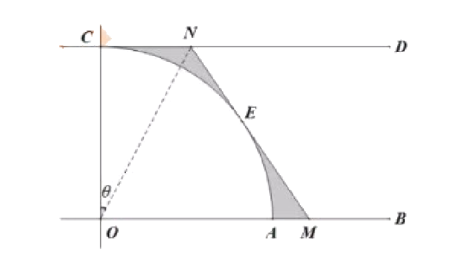
(1)求函数S=f(θ)的解析式,并写出函数的定义域;
(2)为对该计划进行可行性研究,需要预知所建停车场至少有多少面积,请计算当θ为何值时,S有最小值,并求出该最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() C的极坐标方程为
C的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 分别交
分别交![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() .
.
(1)求f(﹣1)+f(3)的值;
(2)求证:f(x+1)为奇函数;
(3)若锐角α满足f(2﹣sinα)+f(cosα)>0,求α的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,求满足方程
时,求满足方程![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在R上的奇函数.
是定义在R上的奇函数.
①若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
②已知函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com