
科目: 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线l和曲线![]() 的普通方程;
的普通方程;
(2)设直线l和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的周期为
的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() ,若先把函数
,若先把函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)设函数![]() ,试判断
,试判断![]() 在
在![]() 内的零点个数.
内的零点个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在梯形ABCD中,DC∥AB,DC⊥CB,E是AB的中点,且AB=2BC=2CD=4(如图所示),将△ADE沿DE翻折,使AB=2(如图所示),F是线段AD上一点,且AF=2DF.
(Ⅰ)求四棱锥A-BCDE的体积;
(Ⅱ)在线段BE上是否存在一点G,使EF∥平面ACG?若存在,请指出点G的位置,并证明你的结论;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: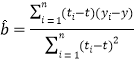 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x.
(1)求f(x)的解析式,并画出f(x)的图象;
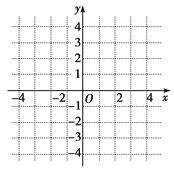
(2)设g(x)=f(x)-k,利用图象讨论:当实数k为何值时,函数g(x)有一个零点?二个零点?三个零点?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
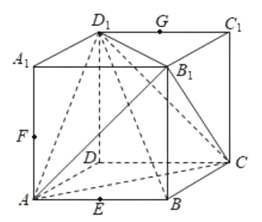
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
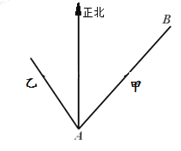
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() ,一动直线l过
,一动直线l过![]() 与圆
与圆![]() 相交于
相交于![]() .两点,
.两点,![]() 是
是![]() 中点,l与直线m:
中点,l与直线m:![]() 相交于
相交于![]() .
.
(1)求证:当l与m垂直时,l必过圆心![]() ;
;
(2)当![]() 时,求直线l的方程;
时,求直线l的方程;
(3)探索![]() 是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关,若无关,请求出其值;若有关,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com