
科目: 来源: 题型:
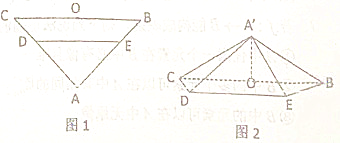
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为推进“千村百镇计划”,2019年4月某新能源公司开展“电动绿色出行”活动,首批投放200台![]() 型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到某地多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为100分).最后该公司共收回有效评分表600份,现从中随机抽取40份(其中男、女的评分表各20份)作为样本,经统计得到茎叶图:
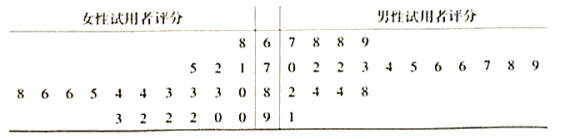
(1)求40个样本数据的中位数![]() ;
;
(2)已知40个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请以40个样本数据的频率分布来估计收回的600份评分表中,评分小于![]() 的份数;
的份数;
②请根据40个样本数据,完成下面2×2列联表:
认定类型 性别 | 满意型 | 需改进型 | 合计 |
女性 | 20 | ||
男性 | 20 | ||
合计 | 40 |
根据2×2列联表判断能否有99%的把握认为“认定类型”与性别有关?
附: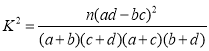 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
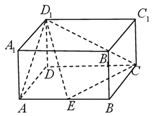
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ) 判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅱ) 设函数![]() 的定义域为
的定义域为![]() ,且有极值点.
,且有极值点.
(ⅰ) 试判断当![]() 时,
时, ![]() 是否满足题目的条件,并说明理由;
是否满足题目的条件,并说明理由;
(ⅱ) 设函数![]() 的极小值点为
的极小值点为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,D是边AC上一点,将
,D是边AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() .若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
.若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围为()
,则x的取值范围为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com