【题目】已知，，对任意，有成立.

（1）求的通项公式；

（2）设，，是数列的前项和，求正整数，使得对任意，恒成立；

（3）设，是数列的前项和，若对任意均有恒成立，求的最小值.

【题目】对于定义在R上函数，有以下四个命题：

（1）直线与的图像的公共点个数一定为1；

（2）若在区间上单调增函数，在上也是单调增函数，则函数在R上一定是单调增函数；

（3）若为奇函数，则一定有；

（4）若，则函数一定不是偶函数.

其中正确的命题序号是_______.（请写出所有正确命题的序号）

（Ⅰ）根据表中数据，建立关于的线性回归方程；

（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.

附:对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为：，.(参考数据:，计算结果保留小数点后两位）

【题目】如图，在长方形ABCD中，AB= ,AD=2,E,F为线段AB的三等分点，G、H为线段DC的三等分点．将长方形ABCD卷成以AD为母线的圆柱W的半个侧面，AB、CD分别为圆柱W上、下底面的直径．

（Ⅰ）证明：平面ADHF⊥平面BCHF；

（Ⅱ）若P为DC的中点，求三棱锥H—AGP的体积．

【题目】函数的值域为_________________．

设平面上向量＝(cosα，sinα) (0°≤α＜360°)，＝(－，)．

(1)试证：向量与垂直；

(2)当两个向量与的模相等时，求角α.

【题目】设等差数列的前项和为，已知，

，则下列结论正确的是（ ）

A. B.

C. D.

(1)在－720°～0°范围内找出所有与角α终边相同的角β；

(2)设集合，判断两集合的关系．

【题目】如图，在四棱锥中，侧面底面ABCD，侧棱，底面ABCD为直角梯形，其中，，，O为AD中点.

（1）求异面直线PB与CD所成角的余弦值；

（2）线段AD上是否存在点Q，使得它到平面PCD的距离为？若存在，求出的值；若不存在，请说明理由.

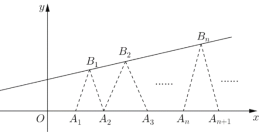
【题目】如图，已知点列、、、、（）依次为函数图像上的点，点列、、、（）依次为轴正半轴上的点，其中（），对于任意，点、、构成一个顶角的顶点为的等腰三角形.

（1）证明：数列是等差数列；

（2）证明：为常数，并求出数列的前项和；

（3）在上述等腰三角形中，是否存在直角三角形？若存在，求出值，若不存在，请说明理由.