
科目: 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,圆心为
,圆心为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线
在直线![]() 上,过
上,过![]() 点作圆
点作圆![]() 的切线
的切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.
(1)若![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:经过![]() ,
,![]() ,
,![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位开展岗前培训期间,甲、乙2人参加了5次考试,成绩统计如下:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 82 | 82 | 79 | 95 | 87 |
乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(1)根据有关统计知识回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适?请说明理由;
(2)根据有关概率知识解答以下问题:若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若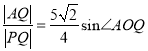 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某小学随机抽取100名学生,将他们的身高(单位:厘米)按照区间 [ 100 , 110),[ 110 , 120),[ 120 , 130),[130 ,140) , [140 , 150] 进行分组,得到频率分布直方图(如图).
(Ⅰ)求直方图中a的值;
(Ⅱ)若要从身高在[ 120 , 130),[130 ,140) , [140 , 150] 三组内的学生中,用分层抽样的方法选取18人参加一项活动,求从身高在[140 ,150]内的学生中应选取的人数;
(Ⅲ)这100名学生的平均身高约为多少厘米?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某运动员毎次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算机产生0到9之间取整数值的随机数,指定1,3,4表示命中,5,6,7,8,9,0表示不命中;再以三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
![]()
据此估计,该运动员三次投篮恰有两次命中的概率为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列命题:
①“数列![]() 为等比数列”是“数列
为等比数列”是“数列![]() 为等比数列”的充分不必要条件;
为等比数列”的充分不必要条件;
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充要条件;
上为增函数”的充要条件;
③“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 互相垂直”的充要条件;
互相垂直”的充要条件;
④设![]() ,
,![]() ,
,![]() 分别是
分别是![]() 三个内角
三个内角![]() ,
,![]() ,
,![]() 所对的边,若
所对的边,若![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件.其中,真命题的序号是________.
”的必要不充分条件.其中,真命题的序号是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国有一道古典数学名著——两鼠穿墙:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”题意是:“有两只老鼠从墙的两边打洞穿墙(连线与墙面垂直),大老鼠第一天进一尺,以后每天加倍,小老鼠第一天也进一尺,以后每天减半,那么两鼠第几天能见面.”假设墙厚16尺,如图是源于该题思想的一个程序框图,则输出的![]() ( )
( )
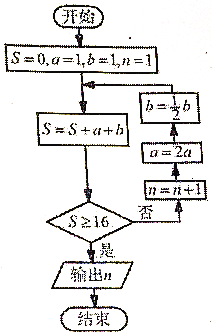
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数![]() 的图象的一部分,后一段DBC是函数
的图象的一部分,后一段DBC是函数![]() 的图象,图象的最高点为
的图象,图象的最高点为 ,且
,且![]() ,垂足为点F.
,垂足为点F.

(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为![]() ,点E在OC上,求儿童乐园的面积.
,点E在OC上,求儿童乐园的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com