
科目: 来源: 题型:
【题目】在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点 ( )
A. 有且只有一个 B. 有且只有三个 C. 有且只有四个 D. 有且只有五个
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目: 来源: 题型:
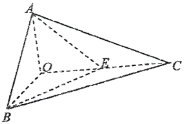
【题目】如图,已知三棱锥O—ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A—BE—C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知O为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(1)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(2)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(3)由(1)中函数![]() 的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移
的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,已知
的图象,已知![]() ,
,![]() ,问在
,问在![]() 的图象上是否存在一点P,使得
的图象上是否存在一点P,使得![]() .若存在,求出P点坐标;若不存在,说明理由.
.若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,其中x>0,k为常数,e为自然对数的底数.
,其中x>0,k为常数,e为自然对数的底数.
(1)当k≤0时,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间(1,3)上存在两个极值点,求实数k的取值范围;
在区间(1,3)上存在两个极值点,求实数k的取值范围;
(3)证明:对任意给定的实数k,存在![]() (
(![]() ),使得
),使得![]() 在区间(
在区间(![]() ,
,![]() )上单调递增.
)上单调递增.
查看答案和解析>>
科目: 来源: 题型:
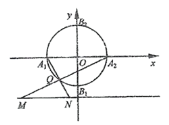
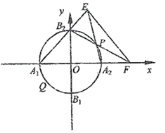
【题目】在平面直角坐标系xOy中,圆O:![]() 与坐标轴分别交于A1,A2,B1,B2(如图).
与坐标轴分别交于A1,A2,B1,B2(如图).
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线![]() 交于不同的两点M,N,求线段MN长的最小值;
交于不同的两点M,N,求线段MN长的最小值;
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设A2P的斜率为k,EF的斜率为m,求证:2m﹣k为定值.
(图1) (图2)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com