
科目: 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程组,解出即可;
的方程组,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用导数研究其单调性可得
, 利用导数研究其单调性可得
![]() ,
,
从而证明![]() .
.
试题解析:((1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;且
单调递增;且![]() ,
,
所以![]() 在
在![]() 上当单调递减,在
上当单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
故![]() ,
,
故![]() .
.
【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】16种食品所含的热量值如下:
111 123 123 164 430 190 175 236
430 320 250 280 160 150 210 123
(1)求数据的中位数与平均数;
(2)用这两种数字特征中的哪一种来描述这个数据集更合适?
查看答案和解析>>
科目: 来源: 题型:
【题目】给出以下四个结论:
①过点![]() ,在两轴上的截距相等的直线方程是
,在两轴上的截距相等的直线方程是![]() ;
;
②若![]() 是等差数列
是等差数列![]() 的前n项和,则
的前n项和,则![]() ;
;
③在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
④已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最大值是2.
的最大值是2.
其中正确的结论是________(写出所有正确结论的番号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
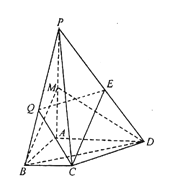
(1)求证:CE//平面BMD
(2)点Q为线段BP中点,求直线PA与平面CEQ所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 设
设![]() 表示p、q中的较大值,
表示p、q中的较大值,![]() 表示p、q中的较小值)记
表示p、q中的较小值)记![]() 的最小值为A,
的最小值为A,![]() 的最大值为B,则A-B=
的最大值为B,则A-B=
A. 16 B. -16 C. a2-2a-16 D. a2+2a-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com