
科目: 来源: 题型:
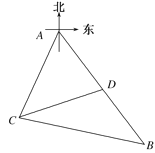
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,
,![]() 分别是椭圆的左、右两焦点,过
分别是椭圆的左、右两焦点,过![]() 且倾斜角为
且倾斜角为![]() (
(![]() )的动直线
)的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(如图所示,点
两点(如图所示,点![]() 在
在![]() 轴上方).当
轴上方).当![]() 时,弦
时,弦![]() 的长为
的长为![]() .
.

(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)若![]() 依次成等差数列,求直线
依次成等差数列,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为![]() 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.

(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 与
与![]() 的相关系数
的相关系数![]() 精确到0.01,并判断
精确到0.01,并判断![]() 与
与![]() 的关系是否可用线性回归方程模型拟合?(规定:
的关系是否可用线性回归方程模型拟合?(规定:![]() 时,可用线性回归方程模型拟合);
时,可用线性回归方程模型拟合);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型
,并对其进行两次检测,当第一次检测合格后,才能进行第二次检测.第一次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:(1)相关系数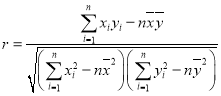
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
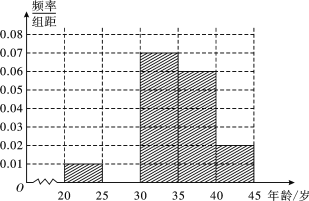
分组(单位:岁) | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校数学学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名,对他们在2018年高考的数学成绩进行调查,统计发现40名新生的数学分数![]() 分布在
分布在![]() 内.当
内.当![]() 时,其频率
时,其频率![]() .
.

(1)求![]() 的值;
的值;
(2)请在答题卡中画出这40名新生高考数学分数的频率分布直方图,并估计这40名新生的高考数学分数的平均数(同一组中的数据用该区间的中点值作代表).
(3)若高考数学分数不低于120分的为优秀,低于120分的为不优秀,则按高考成绩优秀与否从这40名新生中用分层抽样的方法抽取4名学生,再从这4名学生中随机抽取2名,求这2名学生的高考成绩均为优秀的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市收集并整理了该市2019年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.( )

已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论正确的是
A.最低气温与最高气温为正相关B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月D.最低气温低于0 ℃的月份有4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com