（1）求两天全部通过检查的概率；

（2）若厂内对该车间生产的产品质量采用奖惩制度，两天全不通过检查罚300元，通过1天，2天分别奖300元900元.那么该车间在这两天内得到奖金的数学期望是多少元？

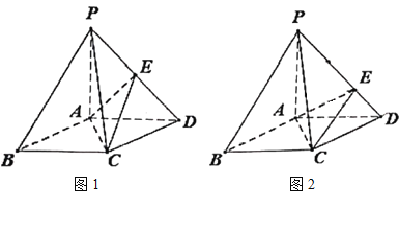
【题目】在底面是菱形的四棱锥中，.

（1）证明：平面；

（2）点在棱上.

①如图1，若点是线段的中点，证明：平面；

②如图2，若，在棱上是否存在点，使得平面？证明你的结论.

【题目】设为非空实数集（至少有两个元素），若对任意，都有，且，则称为封闭集，则下列四个判断：

①集合为封闭集，则为无限集； ②集合为封闭集；

③若集合为封闭集，则为封闭集； ④若为封闭集，则一定有；，

其中正确的命题个数有（ ）.

A.4个B.3个C.2个D.1个

【题目】已知函数f（x）＝sin（）的图象与函数g（x）的图象关于x＝1对称，则函数g（x）在（﹣6，﹣4）上（　　）

A. 单调递增 B. 单调递减 C. 先增后减 D. 先减后增

该电子商务平台将年龄在的人群定义为消费主力军，其它年龄段定义为消费潜力军.

（1）若该电子商务平台共10万位网上购物者，试估计消费主力军的人数；

（2）为了鼓励消费潜力军消费，该平台决定对年消费达到2000元的购物者发放代金券，消费主力军每人发放100元，消费潜力军每人发放200元.现采用分层抽样（按消费主力军与消费潜力军分层）的方式从参与调查的1000位网上购物者中抽取10人，并在这10人中随机抽取3人进行回访，求这3人获得代金券总金额（单位：元）的分布列及数学期望.

（1）画散点图；

（2）如果y对x有线性相关关系，求回归直线方程；

（3）若实际生产中，允许每小时的产品中有缺点的零件最多为89个，那么机器的运转速度应控制在什么范围内？(参考数值：)

【题目】①回归分析中，相关指数的值越大，说明残差平方和越大；

②对于相关系数，越接近1，相关程度越大，越接近0，相关程度越小；

③有一组样本数据得到的回归直线方程为，那么直线必经过点；

④是用来判断两个分类变量是否有关系的随机变量，只对于两个分类变量适合；

以上几种说法正确的序号是__________．

【题目】设奇函数上是增函数，且，则不等式的解集为（ ）

A. B.

C. D.

（1）当m＝0时，（i）求y＝f（x）在（，f（））处的切线方程；

（ii）证明：f（x）＜ex；

（2）当x≥0时，函数f（x）单调递减，求m的取值范围．

【题目】设定义在上的函数、和，满足，且对任意实数、（），恒有成立.

⑴试写 出一组满足条件的具体的和，使为增函数，为减函数，但为增函数.

⑵判断下列两个命题的真假，并说明理由.

命题1）：若为增函数，则为增函数；

命题2）：若为增函数，则为增函数.

⑶已知，写出一组满足条件的具体的和，且为非常值函数，并说明理由.