（1）求二面角P-BD-Q的余弦值；

（2）求点P到平面QBD的距离.

【题目】如图，在四棱锥中，底面为菱形，，，.

（1）求证：平面平面；

（2）若，求直线与平面所成角的正弦值.

【题目】已知函数f(x)=4sincos x+.

(1)求函数f(x)的最小正周期和单调递增区间;

(2)若函数g(x)=f(x)-m区间在上有两个不同的零点x1,x2,求实数m的取值范围,并计算tan(x1+x2)的值.

【题目】已知公差不等于的正项等差数列的前项和为，递增等比数列的前项和为，，，，.

（1）求满足，的的最小值；

（2）求数列的前项和.

A.－1B.1C.2－1D.2

【题目】已知集合是满足下列性质的函数的全体：在定义域内存在实数，使得成立.

（1）已知函数，判断 函数是否属于集合；

（2）若函数属于集合，试求实数的取值范围；

（3） 证明函数属于集合.

【题目】如表提供了工厂技术改造后某种型号设备的使用年限和所支出的维修费（万元）的几组对照数据：

参考公式：，.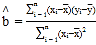

（1）若知道对呈线性相关关系，请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低？

【题目】我校高一年级某研究小组经过调查发现：提高北环隧道的车辆通行能力可有效改善交通状况，在一般情况下，隧道内的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米，车流密度指每千米道路上车辆的数量）的函数.当隧道内的车流密度达到210辆/千米时，将造成堵塞，此时车流速度为0；当车流密度不超过30辆/千米时，车流速度为60千米/小时，研究表明：当时，车流速度是车流密度的一次函数.

（1）求函数的表达式；

（2）当车流密度为多大时，车流量（单位时间内通过某观测点的车辆数，单位：辆/小时） 可以达到最大，并求出最大值.

【题目】已知函数．

若，，试证明：当时，；

若对任意，均有两个极值点，

试求b应满足的条件；

当时，证明：．