
科目: 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,P,Q分别为棱BC和棱CC1的中点,则下列说法正确的是( )
A.BC1//平面AQP
B.平面APQ截正方体所得截面为等腰梯形
C.A1D⊥平面AQP
D.异面直线QP与A1C1所成的角为60°
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.设有一个回归方程![]() ,变量x增加1个单位时,y平均减少5个单位
,变量x增加1个单位时,y平均减少5个单位
C.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),则P(ξ>1)=0.5
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,
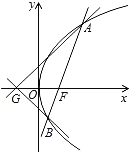
(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定![]() 的单调区间:
的单调区间:
(II)若f(x)在区间![]() (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了![]() 名男生和
名男生和![]() 名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定
名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定![]() 分以上为优分(含
分以上为优分(含![]() 分).
分).

(1)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据列联表判断,能否在犯错误概率不超过![]() 的前提下认为“学科成绩与性别有关”?
的前提下认为“学科成绩与性别有关”?
(2)将频率视作概率,从高二年级该学科成绩中任意抽取![]() 名学生的成绩,求成绩为优分人数
名学生的成绩,求成绩为优分人数![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: .
.
参考数据:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: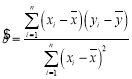 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.从随机抽取的5间服务站中再任取2间作网购商品的调查,则恰有1间是优秀服务站的概率为_____.
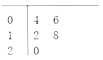
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,若
上的一点,若![]() 平面
平面![]() ,
,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() ,
,![]() .
.
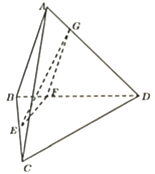
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com