
科目: 来源: 题型:
【题目】某企业有![]() ,
,![]() 两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从
两个分厂生产某种产品,规定该产品的某项质量指标值不低于130的为优质品.分别从![]() ,
,![]() 两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
两厂中各随机抽取100件产品统计其质量指标值,得到如图频率分布直方图:
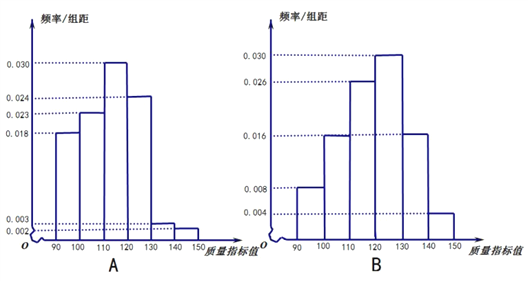
(1)根据频率分布直方图,分别求出![]() 分厂的质量指标值的众数和中位数的估计值;
分厂的质量指标值的众数和中位数的估计值;
(2)填写![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为这两个分厂的产品质量有差异?
的把握认为这两个分厂的产品质量有差异?
优质品 | 非优质品 | 合计 | |
| |||
| |||
合计 |
(3)(i)从![]() 分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
分厂所抽取的100件产品中,利用分层抽样的方法抽取10件产品,再从这10件产品中随机抽取2件,已知抽到一件产品是优质品的条件下,求抽取的两件产品都是优质品的概率;
(ii)将频率视为概率,从![]() 分厂中随机抽取10件该产品,记抽到优质品的件数为
分厂中随机抽取10件该产品,记抽到优质品的件数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某科研小组有20个不同的科研项目,每年至少完成一项。有下列两种完成所有科研项目的计划:
A计划:第一年完成5项,从第一年开始,每年完成的项目不得少于次年,直到全部完成为止;
B计划:第一年完成项数不限,从第一年开始,每年完成的项目不得少于次年,恰好5年完成所有项目。
那么,按照A计划和B计划所安排的科研项目不同完成顺序的方案数量
A. 按照A计划完成的方案数量多
B. 按照B计划完成的方案数量多
C. 按照两个计划完成的方案数量一样多
D. 无法判断哪一种计划的方案数量多
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式: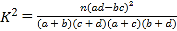
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P(-1,0),设不垂直于x轴的直线l与抛物线y2=2x交于不同的两点A、B,若x轴是∠APB的角平分线,则直线l一定过点
A. (![]() ,0) B. (1,0) C. (2,0) D. (-2,0)
,0) B. (1,0) C. (2,0) D. (-2,0)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向外作正方形
为一边向外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
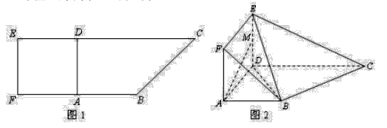
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正![]() 边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出
边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出![]() 的值分别为( )
的值分别为( )
(参考数据:![]() )
)

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com