【题目】已知椭圆与直线都经过点.直线与平行，且与椭圆交于两点，直线与轴分别交于两点.

（1）求椭圆的方程；

（2）证明： 为等腰三角形.

(Ⅰ)应收集多少名女职工样本数据?

(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:，，，，，.试估计该公司职工每周平均上网时间超过4小时的概率是多少?

(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”

A. 平面内的三条直线，若，则.类比推出：空间中的三条直线，若，则

B. 平面内的三条直线，若，则.类比推出：空间中的三条向量，若，则

C. 在平面内，若两个正三角形的边长的比为，则它们的面积比为.类比推出：在空间中，若两个正四面体的棱长的比为，则它们的体积比为

D. 若，则复数.类比推理：“若，则”

备受关注百分比指：一个展区中受到所有相关人士关注简称备受关注的企业数与该展区的企业数的比值．

（1）从企业产品展7个展区的企业中随机选取1家，求这家企业是选自“智能及高端装备”展区备受关注的企业的概率；

（2）某电视台采用分层抽样的方法，在“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中抽取6家进行了采访，若从受访企业中随机抽取2家进行产品展示，求恰有1家来自于“医疗器械及医药保健”展区的概率．

【题目】已知从有限个平面向量构成的集合中任取三个元素，其中总存在两个元素，使得.试求中元素个数的最大值.

【题目】空气质量指数（，简称）是定量描述空气质量状况的指数，空气质量按照大小分为六级：为优；为良；为轻度污染；为中度污染；为重度污染；为严重污染.一环保人士记录去年某地某月10天的的茎叶图如下.

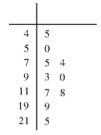
（1）利用该样本估计该地本月空气质量优良（）的天数；（按这个月总共30天计算）

（2）将频率视为概率，从本月中随机抽取3天，记空气质量优良的天数为，求的概率分布列和数学期望.

【题目】如图，正六边形的中心为，对、、、、、、这七个点中的任意两点，以其中一点为起点、另一点为终点作向量.任取其中两个向量，以它们的数量积的绝对值作为随机变量.试求的概率分布列及其数学期望.

【题目】已知函数，其中．

（1）若，求曲线在点处的切线方程；

（2）求在上的最小值．

（1）当a＝1时，求f(x)的单调递增区间；

（2）若f(x)的极大值是6e-2，求a的值．

【题目】（本小题满分14分）已知函数．

（Ⅰ）求函数的单调递增区间；

（Ⅱ）证明：当时，；

（Ⅲ）确定实数的所有可能取值，使得存在，当时，恒有．